
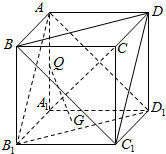
 如图,ABCD-A1B1C1D1是棱长为a的正方体,有下列说法:
如图,ABCD-A1B1C1D1是棱长为a的正方体,有下列说法:分析 根据正方体的几何特征,逐一分析和判断四个命题的真假,综合讨论结果,可得答案.
解答 解:∵ABCD-A1B1C1D1是棱长为a的正方体,
①若点P在△BDC1所在平面上运动,则三棱锥P-AB1D1的高为定值$\frac{\sqrt{3}}{3}a$,底面AB1D1的面积为定值$\frac{\sqrt{3}}{2}{a}^{2}$,故三棱锥P-AB1D1的体积为定值$\frac{1}{6}{a}^{3}$,故正确;
②若点M、N、L分别是棱A1B1、A1D、A1A上与端点不重合的三个动点,则△MNL必为锐角三角形,故正确;
③若点Q为A1A的中点,点G为正方形A1B1C1D1(包含边界)内一个动点,且始终满足GQ⊥A1C,则动点Q的连接A1B1,A1D1中点的线段,故错误;
④若M∈线段A1C(除端点A1、C外),A1C⊥平面α截正方体得到的截面是不同的多边形,则这些不同的多边形只能是三角形或六边形,
当M落在线段A1C的中点上时,它们的面积和周长取最大值,分别为$\frac{3\sqrt{3}}{4}$a2和3$\sqrt{2}$a,故正确.
综上所述,正确的说法是:①④,
故答案为:①②④
点评 本题以命题的真假判断与应用为载体,考查了正方体的几何特征,棱锥的体积,三角形形状的判断,难度中档.


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | (0,2] | C. | {0,1,2} | D. | {1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a1≥-5 | B. | a1≥-1 | C. | a1≥-1或a1≤-5 | D. | 以上都不对 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com