
分析 (Ⅰ)由动点P到点($\frac{1}{2}$,0)的距离比它到直线x=-$\frac{5}{2}$的距离小2,可得动点P到点($\frac{1}{2}$,0)的距离与它到直线x=-$\frac{1}{2}$的距离相等,由此能求出抛物线方程.
(Ⅱ)设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),则k2=$\frac{{y}_{4}-{y}_{3}}{{x}_{4}-{x}_{3}}$=$\frac{2}{{y}_{4}+{y}_{3}}$=-$\frac{{y}_{1}{y}_{2}}{{y}_{1}+{y}_{2}}$=2k1,即可得出结论.
解答 (Ⅰ)解:∵动点P到点($\frac{1}{2}$,0)的距离比它到直线x=-$\frac{5}{2}$的距离小2,
∴动点P到点($\frac{1}{2}$,0)的距离与它到直线x=-$\frac{1}{2}$的距离相等,
∴动点P的轨迹是以点($\frac{1}{2}$,0)为焦点的抛物线,
∴动点P的轨迹方程为y2=2x;
(Ⅱ)证明:设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),
则直线AB的方程为y=k1(x-2),代入抛物线方程中,得${y}^{2}-\frac{2y}{{k}_{1}}-4=0$,
∴y1+y2=$\frac{2}{{k}_{1}}$,y1y2=-4
直线AC,BD过点Q(1,0),同理可得y1y3=y2y4=-2,
∴y3=-$\frac{2}{{y}_{1}}$,${y}_{4}=-\frac{2}{{y}_{2}}$,
∴k2=$\frac{{y}_{4}-{y}_{3}}{{x}_{4}-{x}_{3}}$=$\frac{2}{{y}_{4}+{y}_{3}}$=-$\frac{{y}_{1}{y}_{2}}{{y}_{1}+{y}_{2}}$=2k1,
∴$\frac{{k}_{2}}{{k}_{1}}$=2.
点评 本题考查抛物线方程的求法,考查两直线的斜率的比值是否为定值的判断与求法,解题时要认真审题,注意直线方程的合理运用.


科目:高中数学 来源: 题型:选择题
 《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑,如图,网格纸上正方形小格的边长为1,图中粗线画出的是某几何体毛坯的三视图,第一次切削,将该毛坯得到一个表面积最大的长方体,第二次切削沿长方体的对角面刨开,得到两个三棱柱,第三次切削将两个三棱柱分别沿棱和表面的对角线刨开得到两个鳖臑和两个阳马,则阳马与鳖臑的体积之比为( )
《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑,如图,网格纸上正方形小格的边长为1,图中粗线画出的是某几何体毛坯的三视图,第一次切削,将该毛坯得到一个表面积最大的长方体,第二次切削沿长方体的对角面刨开,得到两个三棱柱,第三次切削将两个三棱柱分别沿棱和表面的对角线刨开得到两个鳖臑和两个阳马,则阳马与鳖臑的体积之比为( )| A. | 3:1 | B. | 2:1 | C. | 1:1 | D. | 1:2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9 | B. | 3 | C. | $\sqrt{109}$ | D. | 3$\sqrt{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,1,2} | B. | {1,2} | C. | {0} | D. | {0,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
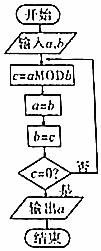 “欧几里得算法”是有记载的最古老的算法,可追溯至公元前300年前,如图的程序框图的算法思路就是来源于“欧几里得算法”.执行改程序框图(图中“aMODb”表示a除以b的余数),若输入的a,b分别为675,125,则输出的a=( )
“欧几里得算法”是有记载的最古老的算法,可追溯至公元前300年前,如图的程序框图的算法思路就是来源于“欧几里得算法”.执行改程序框图(图中“aMODb”表示a除以b的余数),若输入的a,b分别为675,125,则输出的a=( )| A. | 0 | B. | 25 | C. | 50 | D. | 75 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 11 | C. | 12 | D. | 6+$\sqrt{29}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ±$\frac{4\sqrt{2}}{9}$ | B. | $\frac{7}{9}$ | C. | -$\frac{4\sqrt{2}}{9}$ | D. | -$\frac{7}{9}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com