
【题目】如图,在四棱锥P—ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,AB=4,PA=3,点A在PD上的射影为点G,点E在AB上,平面PEC⊥平面PDC.
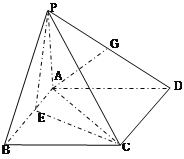
(1)求证:AG∥平面PEC;
(2)求AE的长;
(3)求二面角E—PC—A的正弦值.
【答案】(1)见解析.(2)![]() (3)
(3)![]() .
.
【解析】
试题解(1)证明:∵CD⊥AD,CD⊥PA
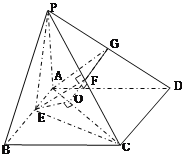
∴CD⊥平面PAD ∴CD⊥AG,
又PD⊥AG
∴AG⊥平面PCD
作EF⊥PC于F,因面PEC⊥面PCD
∴EF⊥平面PCD,
∴EF∥AG
又AG![]() 面PEC,EF
面PEC,EF![]() 面PEC,
面PEC,
∴AG∥平面PEC
(2)由(Ⅰ)知A、E、F、G四点共面,又AE∥CD,
∴AE∥平面PCD.
∴AE∥GF.
∴四边形AEFG为平行四边形,∴AE=GF.
∵PA=3,AB=4,∴PD=5,AG=![]() ,
,
又PA2=PGPD,∴PG![]()
又![]() ,∴
,∴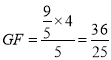 ,∴
,∴![]()
(3)过E作EO⊥AC于点O,易知EO⊥平面PAC,
又EF⊥PC,∴OF⊥PC∴∠EFO即为二面角E—PC—A的平面角
![]() ,
,
又EF=AG![]()
∴![]()


科目:高中数学 来源: 题型:
【题目】某宾馆在装修时,为了美观,欲将客房的窗户设计成半径为![]() 的圆形,并用四根木条将圆分成如图所示的9个区域,其中四边形
的圆形,并用四根木条将圆分成如图所示的9个区域,其中四边形![]() 为中心在圆心的矩形,现计划将矩形
为中心在圆心的矩形,现计划将矩形![]() 区域设计为可推拉的窗口.
区域设计为可推拉的窗口.
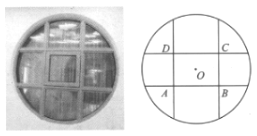
(1)若窗口![]() 为正方形,且面积大于
为正方形,且面积大于![]() (木条宽度忽略不计),求四根木条总长的取值范围;
(木条宽度忽略不计),求四根木条总长的取值范围;
(2)若四根木条总长为![]() ,求窗口
,求窗口![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图为某班35名学生的投篮成绩(每人投一次)的条形统计图,其中上面部分数据破损导致数据不完全。已知该班学生投篮成绩的中位数是5,则根据统计图,则下列说法错误的是( )

A. 3球以下(含3球)的人数为10
B. 4球以下(含4球)的人数为17
C. 5球以下(含5球)的人数无法确定
D. 5球的人数和6球的人数一样多
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 的顶点为
的顶点为![]() ,左、右焦点分别为
,左、右焦点分别为![]() 、
、![]() ,过点A且斜率为
,过点A且斜率为![]() 的直线与y轴交于点P,与椭圆交于另一个点B,且点B在x轴上的射影恰好为点
的直线与y轴交于点P,与椭圆交于另一个点B,且点B在x轴上的射影恰好为点![]() .
.
(1)求椭圆C的标准方程;
(2)M为椭圆C上一动点,![]() 是椭圆C长轴上的一个点,直线MQ与椭圆C的另一个交点为N,令
是椭圆C长轴上的一个点,直线MQ与椭圆C的另一个交点为N,令![]() ,若t值与点M的位置无关,则称此时的点Q为“稳定点”,试求出所有“稳定点”,若没有,请说明理由.
,若t值与点M的位置无关,则称此时的点Q为“稳定点”,试求出所有“稳定点”,若没有,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com