
| A. | 当且仅当x∈(-∞,1),f(x)<0 | B. | 当且仅当x∈(1,+∞),f(x)>0 | ||
| C. | 对于?x∈R,f(x)<0 | D. | 对于?x∈R,f(x)>0 |
分析 f(x)是定义在R上的减函数,f′(x)<0,(f′(x)≠0).则$\frac{f(x)}{f'(x)}<1-x$,化为f(x)+f′(x)x>f′(x),可得[(x-1)f(x)]′>0,因此函数y=(x-1)f(x)在R上单调递增,对x分类讨论即可得出.
解答 解:∵f(x)是定义在R上的减函数,f′(x)<0,(f′(x)≠0).
∴$\frac{f(x)}{f'(x)}<1-x$,化为f(x)+f′(x)x>f′(x),
∴f(x)+f′(x)(x-1)>0,
∴[(x-1)f(x)]′>0,
∴函数y=(x-1)f(x)在R上单调递增,
而x=1时,y=0,则x<1时,y<0,
当x∈(1,+∞)时,x-1>0,故f(x)>0,
又f(x)是定义在R上的减函数,
∴x≤1时,f(x)>0也成立,
∴f(x)>0对任意x∈R成立.
故选:D.
点评 本题考查了利用导数研究函数的单调性、不等式的性质与解法,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
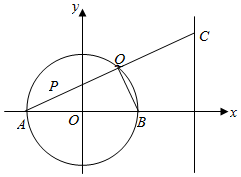 已知圆O:x2+y2=9,直线l1:x=6,圆O与x轴相交于点A,B(如图),点P(-1,2)是圆O内一点,点Q为圆O上任一点(异于点A、B),直线AQ与l1相交于点C.
已知圆O:x2+y2=9,直线l1:x=6,圆O与x轴相交于点A,B(如图),点P(-1,2)是圆O内一点,点Q为圆O上任一点(异于点A、B),直线AQ与l1相交于点C.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
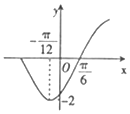 设函数f(x)=cos2x-$\sqrt{3}$sin2x,把y=f(x)的图象向左平移$φ({|φ|<\frac{π}{2}})$个单位后,得到的部分图象如图所示,则f(φ)的值等于( )
设函数f(x)=cos2x-$\sqrt{3}$sin2x,把y=f(x)的图象向左平移$φ({|φ|<\frac{π}{2}})$个单位后,得到的部分图象如图所示,则f(φ)的值等于( )| A. | $-\sqrt{3}$ | B. | $\sqrt{3}$ | C. | -1 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x1>x2 | B. | x1<x2 | C. | ${x}_{1}^{2}$<${x}_{2}^{2}$ | D. | x1+x2=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∨(?q) | B. | (?p)∧q | C. | p∧q | D. | (?p)∧(?q) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{7}$ | B. | $\frac{1}{35}$ | C. | $\frac{8}{35}$ | D. | $\frac{7}{24}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}+i$ | B. | $\sqrt{2}-i$ | C. | $1+\sqrt{2}i$ | D. | $1-\sqrt{2}i$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com