
| A. | G=N+,⊕为整数的加法 | B. | G=N,⊕为整数的加法 | ||
| C. | G=Z,⊕为整数的减法 | D. | G={x|x=2n,n∈Z},⊕为整数的乘法 |
分析 根据题意依次判断各项即可.
解答 解:对于A:任意正数a,b知道:a+b仍为正数,故有a⊕b∈G;但是不存在e∈G,使对一切a∈G都有a⊕e=e⊕a=a,故A的G不是“融洽集.
对于B:根据题意我们可知当a,b都为非负整数时,a,b通过加法运算还是非负整数,且存在一整数0∈G有0+a=a+0=a,所以B为融洽集;
对于C:任意整数a,b知道:a-b仍为整数,故有a⊕b∈G;但是不存在e∈G,使对一切a∈G都有a-e=e-a=a,故C的G不是“融洽集.
对于D:任意偶数a,b知道:ab仍为偶数,故有a⊕b∈G;但是不存在e∈G,使对一切a∈G都有a⊕e=e⊕a=a,故D的G不是“融洽集,不满足存在e∈G,使得对一切a∈G,都有a⊕e=e⊕a=a.
故选B.
点评 本题考查了对题目的理解和存在性的判断.属于中档题.


科目:高中数学 来源: 题型:解答题
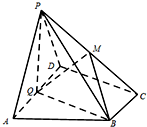 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=$\frac{1}{2}$AD=1,CD=$\sqrt{3}$.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=$\frac{1}{2}$AD=1,CD=$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{27}$ | C. | $\frac{1}{18}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 函数f(x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<0,x∈R)的部分图象如图所示.
函数f(x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<0,x∈R)的部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{3}{4}$,1) | B. | [$\frac{3}{4}$,1) | C. | [$\frac{3}{4}$,1] | D. | (0,1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com