
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 圆C:(x-3)2+(y-4)2=1的圆心C(3,4),半径r=1,设P(a,b)在圆C上,运用向量的加减和数量积运算可得,m2=a2+b2=|OP|2,m的最值即为|OP|的最值,由圆上一点与圆外一点的距离的最值性质,即最值为d±r,即可得到所求差.
解答 解:圆C:(x-3)2+(y-4)2=1的圆心C(3,4),半径r=1,
设P(a,b)在圆C上,则$\overrightarrow{AP}$=(a+m,b),$\overrightarrow{BP}$=(a-m,b),
由$\overrightarrow{AP}$•$\overrightarrow{BP}$=0,
可得(a+m)(a-m)+b2=0,
即m2=a2+b2=|OP|2,
m的最大值即为|OP|的最大值,等于|OC|+r=5+1=6.
m的最小值即为|OP|的最小值,等于|OC|-r=5-1=4.
则m的最大值与最小值之差为6-4=2.
故选:B.
点评 本题考查实数的最值的求法,是中档题,解题时要认真审题,注意向量数量积的坐标表示和两点距离公式的运用,以及圆上一点与圆外一点的距离的最值性质是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
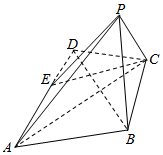 如图,在四边形ABCD中,AB=AD=4,BC=CD=$\sqrt{7}$,点E为线段AD上的一点.现将△DCE沿线段EC翻折到PEC(点D与点P重合),使得平面PAC⊥平面ABCE,连接PA,PB.
如图,在四边形ABCD中,AB=AD=4,BC=CD=$\sqrt{7}$,点E为线段AD上的一点.现将△DCE沿线段EC翻折到PEC(点D与点P重合),使得平面PAC⊥平面ABCE,连接PA,PB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com