
分析 (1)根据“Z函数”的定义,结合分段函数的性质作出图象进行判断即可.
(2)结合“Z函数”的定义以及根式的性质利用配方法进行判断求解.
(3)求出h(x)的解析式以及作出函数h(x)的图象,讨论变量的取值范围解方程即可.
解答 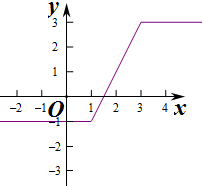 解:(1)f1(x)=|x-1|-|x-3|+1=$\left\{\begin{array}{l}{-1}&{x≤1}\\{2x-3}&{1<x<3}\\{3}&{x≥3}\end{array}\right.$,
解:(1)f1(x)=|x-1|-|x-3|+1=$\left\{\begin{array}{l}{-1}&{x≤1}\\{2x-3}&{1<x<3}\\{3}&{x≥3}\end{array}\right.$,
作出函数f1(x)的图象如图:
当x≤1时,f(x)=-1,当x≥3时,f(x)=3,
当1<x<3时,-1<f(x)<3恒成立,
故f1(x)=|x-1|-|x-3|+1是R上的“Z函数”,
f2(x)=x-|x-2|=$\left\{\begin{array}{l}{2}&{x>2}\\{2x-2}&{x≤2}\end{array}\right.$,
则当x≤2时,函数f(x)不是常数,不满足条件.②,故f2(x)=x-|x-2|不是R上的“Z函数”.
(2)若g(x)=|x-2|-$\sqrt{{x^2}+mx+4}$是R上的“Z函数”,则满足g(x)=|x-2|-|x+a|的形式,
若$\sqrt{{x^2}+mx+4}$=|x+a|,则平方得mx+4=2ax+a2,即$\left\{\begin{array}{l}{a=2}\\{m=4}\end{array}\right.$或$\left\{\begin{array}{l}{a=-2}\\{m=-4}\end{array}\right.$,
当$\left\{\begin{array}{l}{a=-2}\\{m=-4}\end{array}\right.$时,g(x)=|x-2|-|x-2|=0,不满足条件③,故此时g(x)不是“Z函数”,
当$\left\{\begin{array}{l}{a=2}\\{m=4}\end{array}\right.$时,g(x)=|x-2|-|x+2|=$\left\{\begin{array}{l}{4}&{x≤-2}\\{-2x}&{-2<x<2}\\{-4}&{x≥2}\end{array}\right.$,满足条件①②③,故此时g(x)是“Z函数”,
故当m=4时,g(x)为R上的“Z函数”.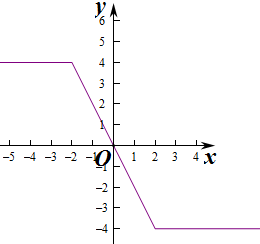
(3)设f(x)是(1)中的“Z函数”,则f(x)=|x-1|-|x-3|+1=$\left\{\begin{array}{l}{-1}&{x≤1}\\{2x-3}&{1<x<3}\\{3}&{x≥3}\end{array}\right.$,
则h(x)=|f(x)|=$\left\{\begin{array}{l}{1}&{x≤1}\\{-2x+3}&{1<x≤\frac{3}{2}}\\{2x-3}&{\frac{3}{2}<x<3}\\{3}&{x≥3}\end{array}\right.$,对应的图象如图: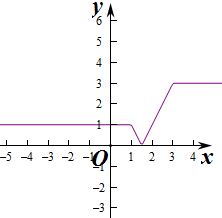
若h(2a2+a)=h(4a),
则①$\left\{\begin{array}{l}{2{a}^{2}+a≤1}\\{4a≤1}\end{array}\right.$,即$\left\{\begin{array}{l}{-1≤a≤\frac{1}{2}}\\{a≤\frac{1}{4}}\end{array}\right.$,即-1≤a≤$\frac{1}{4}$时,h(2a2+a)=h(4a)=1,
②$\left\{\begin{array}{l}{2{a}^{2}+a≥3}\\{4a≥3}\end{array}\right.$得$\left\{\begin{array}{l}{a≥1或a≤-\frac{3}{2}}\\{a≥\frac{3}{4}}\end{array}\right.$即a≥1时,h(2a2+a)=h(4a)=3,
③$\left\{\begin{array}{l}{2{a}^{2}+a≤1}\\{4a=2}\end{array}\right.$或$\left\{\begin{array}{l}{4a≤1}\\{2{a}^{2}+a=2}\end{array}\right.$,此时h(2a2+a)=h(4a)=1,
即$\left\{\begin{array}{l}{-1≤a≤\frac{1}{2}}\\{a=\frac{1}{2}}\end{array}\right.$或$\left\{\begin{array}{l}{a≤\frac{1}{4}}\\{a=\frac{-1±\sqrt{17}}{4}}\end{array}\right.$,即a=$\frac{1}{2}$或a=$\frac{-1-\sqrt{17}}{4}$.
④2a2+a=4a,即2a2=3a,得a=0或a=$\frac{3}{2}$,
综上-1≤a≤$\frac{1}{4}$或a≥1或=$\frac{1}{2}$或a=$\frac{-1-\sqrt{17}}{4}$.
点评 本题主要考查分段函数的应用,结合函数的大小,利用分类讨论以及数形结合的思想进行求解,综合性较强,难度较大.


 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:高中数学 来源: 题型:选择题
| A. | c>b>a | B. | b>c>a | C. | a>c>b | D. | a>b>c |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,e2-1) | B. | (e2-1,+∞) | C. | (0,e2+1) | D. | (e2+1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
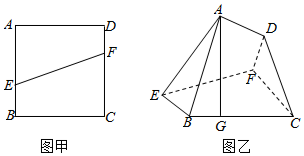 如图甲,设正方形ABCD的边长为3,点E,F分别在AB,CD上,并且满足AE=2EB,CF=2FD,如图乙,将直角梯形AEFD沿EF折到A1EFD1的位置,使点A1在平面EBCF上的射影G恰好在BC上.M点为EA1的中点.
如图甲,设正方形ABCD的边长为3,点E,F分别在AB,CD上,并且满足AE=2EB,CF=2FD,如图乙,将直角梯形AEFD沿EF折到A1EFD1的位置,使点A1在平面EBCF上的射影G恰好在BC上.M点为EA1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9 | B. | 18 | C. | 27 | D. | 36 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com