
| A. | (0,e2-1) | B. | (e2-1,+∞) | C. | (0,e2+1) | D. | (e2+1,+∞) |
分析 求出f(x)的导数,讨论0<x<1,x>1,可得单调性、最值,画出f(x)的图象,由题意可得m>0,令t=f(x1)=f(x3)=g(x2),可得直线y=t与y=g(x)的图象交点在y=f(x)的图象上方,可得m的范围.
解答 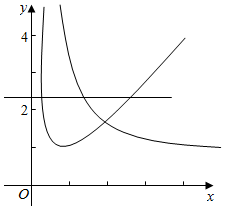 解:函数f(x)=x-$\frac{lnx}{x}$的导数为f′(x)=1-$\frac{1-lnx}{{x}^{2}}$=$\frac{{x}^{2}-1+lnx}{{x}^{2}}$,
解:函数f(x)=x-$\frac{lnx}{x}$的导数为f′(x)=1-$\frac{1-lnx}{{x}^{2}}$=$\frac{{x}^{2}-1+lnx}{{x}^{2}}$,
当0<x<1时,x2-1<0,lnx<0,f′(x)<0,f(x)递减;
当x>1时,x2-1>0,lnx>0,f′(x)>0,f(x)递增.
可得f(x)在x=1处取得极小值,且为最小值1.
作出y=f(x)的图象.
由题意可得f(x)在[e,+∞)递增,且f(x)≥f(e)=e-$\frac{1}{e}$.
任意x3≥e,存在0<x1<x2<x3,使得f(x1)=f(x3)=g(x2),
可得f(x1)=f(x3)=g(x2)≥e-$\frac{1}{e}$.
令t=f(x1)=f(x3)=g(x2),
则m>0,直线y=t与y=g(x)的图象交点在y=f(x)的图象上方.
即有$\frac{m}{e}$<e-$\frac{1}{e}$,解答m<e2-1,
则m的范围是(0,e2-1).
故选:A.
点评 本题考查任意性和存在性问题的解法,考查导数的运用:求单调区间和极值、最值,画出图象,通过数形结合的思想方法是解题的关键,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | {x|x≥-2} | B. | {x|x>-1} | C. | {x|x<-1} | D. | {x|x≤-2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
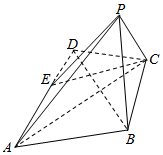 如图,在四边形ABCD中,AB=AD=4,BC=CD=$\sqrt{7}$,点E为线段AD上的一点.现将△DCE沿线段EC翻折到PEC(点D与点P重合),使得平面PAC⊥平面ABCE,连接PA,PB.
如图,在四边形ABCD中,AB=AD=4,BC=CD=$\sqrt{7}$,点E为线段AD上的一点.现将△DCE沿线段EC翻折到PEC(点D与点P重合),使得平面PAC⊥平面ABCE,连接PA,PB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
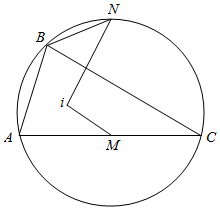 如图所示.在△ABC中,已知AB<BC,点I为其内心,M为边AC上的中点,N为外接圆的弧$\widehat{ABC}$的中点.证明:∠IMA=∠INB.
如图所示.在△ABC中,已知AB<BC,点I为其内心,M为边AC上的中点,N为外接圆的弧$\widehat{ABC}$的中点.证明:∠IMA=∠INB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com