
分析 (Ⅰ)通过讨论x的范围,去掉绝对值号,得到关于x的不等式组,求出m的值即可;(Ⅱ)根据基本不等式的性质得到关于t的方程,解出即可.
解答 解:(Ⅰ)由|x+3|<2x+1得,
$\left\{\begin{array}{l}{x≤-3}\\{-(x+3)<2x+1}\end{array}\right.$或$\left\{\begin{array}{l}{x>-3}\\{x+3<2x+1}\end{array}\right.$,
解得x>2,
依题意m=2.
(Ⅱ)∵|x-t|+|x+$\frac{1}{t}$|≥|x-t-x-$\frac{1}{t}$|=|t|+$\frac{1}{|t|}$,
当且仅当(x-t)(x+$\frac{1}{t}$)≥0时取等号,
因为关于x的方程|x-t|+|x+$\frac{1}{t}$|=2有实数根,
所以|t|+$\frac{1}{|t|}$≤2,另一方面|t|+$\frac{1}{|t|}$≥2,
所以|=|t|+$\frac{1}{|t|}$=2,
所以t=1或t=-1.
点评 本小题考查绝对值不等式的解法与性质、不等式的证明等基础知识,考查运算求解能力、推理论证能力,考查分类与整合思想、化归与转化思想等.


科目:高中数学 来源: 题型:选择题
| A. | c>b>a | B. | b>c>a | C. | a>c>b | D. | a>b>c |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
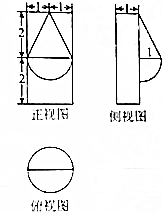 某几何体的三视图如图所示,该几何体的表面积为( )
某几何体的三视图如图所示,该几何体的表面积为( )| A. | 6+$\frac{11+\sqrt{3}}{4}$π | B. | 6+$\frac{13+\sqrt{3}}{2}$π | C. | 6+$\frac{9+\sqrt{5}}{2}$π | D. | 6+$\frac{11+\sqrt{5}}{2}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,e2-1) | B. | (e2-1,+∞) | C. | (0,e2+1) | D. | (e2+1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
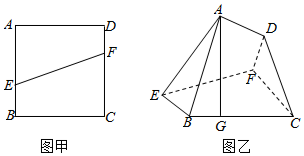 如图甲,设正方形ABCD的边长为3,点E,F分别在AB,CD上,并且满足AE=2EB,CF=2FD,如图乙,将直角梯形AEFD沿EF折到A1EFD1的位置,使点A1在平面EBCF上的射影G恰好在BC上.M点为EA1的中点.
如图甲,设正方形ABCD的边长为3,点E,F分别在AB,CD上,并且满足AE=2EB,CF=2FD,如图乙,将直角梯形AEFD沿EF折到A1EFD1的位置,使点A1在平面EBCF上的射影G恰好在BC上.M点为EA1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9 | B. | 18 | C. | 27 | D. | 36 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com