
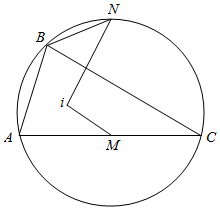
 如图所示.在△ABC中,已知AB<BC,点I为其内心,M为边AC上的中点,N为外接圆的弧$\widehat{ABC}$的中点.证明:∠IMA=∠INB.
如图所示.在△ABC中,已知AB<BC,点I为其内心,M为边AC上的中点,N为外接圆的弧$\widehat{ABC}$的中点.证明:∠IMA=∠INB. 分析 连接NM并延长,交圆O与点P,连接BP交AC于H,由鸡爪定理可得PA=PI,利用相似三角形的性质可证∠PIM=∠PNI,利用四点共圆可证∠PHM=∠PNB,等角减去等角即可证明∠IMA=∠INB.
解答 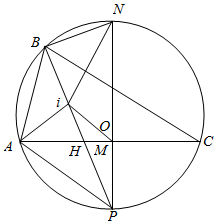 证明:连接NM并延长,交圆O与点P,易知N,O,M,P共线,
证明:连接NM并延长,交圆O与点P,易知N,O,M,P共线,
连接BP交AC于H,易知B,I,H,P共线,
由鸡爪定理,PA=PI,
而PA2=PM•PN,∴PI2=PM•PN,
∴△PIM∽△PNI,∴∠PIM=∠PNI,
又∠HBN=∠HMN=90°,∴B,H,M,N四点共圆,
∴∠PHM=∠PNB,
∴∠IMA=∠INB(等角减去等角).
点评 本题主要考查了鸡爪定理,相似三角形的性质,四点共圆的性质的应用,考查了转化思想和数形结合思想的运用,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 2016 | B. | 4032 | C. | 4026 | D. | 2013 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,e2-1) | B. | (e2-1,+∞) | C. | (0,e2+1) | D. | (e2+1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
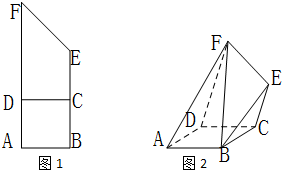 直角梯形ABEF中,BE∥AF,∠FAB=90°,AF=$\frac{3}{2}$BE=3AB=3,C,D分别是边BE,AF上的点(不是端点),且CD⊥AF,如图1所示;现沿CD把直角梯形ABEF折成一个120°的二面角,连接部分线段后围成一个空间几何体,如图2所示.
直角梯形ABEF中,BE∥AF,∠FAB=90°,AF=$\frac{3}{2}$BE=3AB=3,C,D分别是边BE,AF上的点(不是端点),且CD⊥AF,如图1所示;现沿CD把直角梯形ABEF折成一个120°的二面角,连接部分线段后围成一个空间几何体,如图2所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
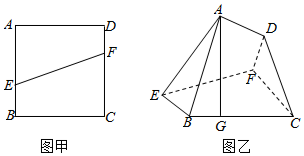 如图甲,设正方形ABCD的边长为3,点E,F分别在AB,CD上,并且满足AE=2EB,CF=2FD,如图乙,将直角梯形AEFD沿EF折到A1EFD1的位置,使点A1在平面EBCF上的射影G恰好在BC上.M点为EA1的中点.
如图甲,设正方形ABCD的边长为3,点E,F分别在AB,CD上,并且满足AE=2EB,CF=2FD,如图乙,将直角梯形AEFD沿EF折到A1EFD1的位置,使点A1在平面EBCF上的射影G恰好在BC上.M点为EA1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com