
| A. | 2016 | B. | 4032 | C. | 4026 | D. | 2013 |
分析 分别表示出anan+1an+2=an+an+1+an+2,an+1an+2an+3=an+1+an+2+an+3,两式相减可推断出an+3=an,进而可知数列{an}是以3为周期的数列,根据数列的周期性进行求解即可.
解答 解:依题意可知,anan+1an+2=an+an+1+an+2,an+1an+2an+3=an+1+an+2+an+3,
两式相减得an+1an+2(an+3-an)=an+3-an,
∵an+1an+2≠1,
∴an+3-an=0,即an+3=an,
∴数列{an}是以3为周期的数列,
∵a1a2a3=a1+a2+a3,∴a3=3
∴S2016=672×(a1+a2+a3)=672×(1+2+3)=672×6=4032,
故选:B.
点评 本题主要考查了数列的递推式和数列的求和问题.本题的关键是找出数列的周期性.考查学生的推理能力.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{a}$>$\frac{1}{b}$ | B. | $\frac{1}{a-b}$>$\frac{1}{a}$ | C. | a3<b3 | D. | |a|>|b| |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x≥-2} | B. | {x|x>-1} | C. | {x|x<-1} | D. | {x|x≤-2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1,1} | B. | [-1,1] | C. | {-1,-3,1,3} | D. | {-3,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=log2x+logx2(0<x<1) | B. | y=$\frac{{x}^{2}+3}{\sqrt{{x}^{2}+2}}$ | ||
| C. | y=ex+e-x | D. | y=x+$\frac{1}{x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
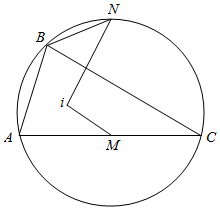 如图所示.在△ABC中,已知AB<BC,点I为其内心,M为边AC上的中点,N为外接圆的弧$\widehat{ABC}$的中点.证明:∠IMA=∠INB.
如图所示.在△ABC中,已知AB<BC,点I为其内心,M为边AC上的中点,N为外接圆的弧$\widehat{ABC}$的中点.证明:∠IMA=∠INB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com