
分析 (1)求出函数的导数,通过讨论m的范围,求出函数的单调区间即可;
(2)问题等价于对任意的m∈(4,6),恒有(a+ln3)(2-m)-2ln3>5-2m-mln3-$\frac{1}{3}$-12+6m成立,即(2-m)a>$\frac{2}{3}$-4(2-m),根据m>2,分离a,从而求出a的范围即可.
解答 解:(1)函数定义域为(0,+∞),
$f'(x)=\frac{m}{x}-\frac{1}{x^2}+4-2m=\frac{(2x-1)[(2-m)x+1]}{x^2}$.
令f′(x)=0,得x1=$\frac{1}{2}$,${x_2}=-\frac{1}{2-m}$,
当m=4时,f'(x)≤0,函数f(x)的在定义域(0,+∞)单调递减;
当2<m<4时,由f'(x)>0,得$\frac{1}{2}<x<-\frac{1}{2-m}$;由f′(x)<0,得$0<x<\frac{1}{2}$或$x>-\frac{1}{2-m}$,
所以函数f(x)的单调递增区间为$(\frac{1}{2},-\frac{1}{2-m})$,递减区间为$(0,\frac{1}{2})$,$(-\frac{1}{2-m},+∞)$;
当m>4时,由f'(x)>0,得$-\frac{1}{2-m}<x<\frac{1}{2}$;由f′(x)<0,得$0<x<-\frac{1}{2-m}$或$x>\frac{1}{2}$,
所以函数f(x)的单调递增区间为$(-\frac{1}{2-m},\frac{1}{2})$,递减区间为$(0,-\frac{1}{2-m})$,$(\frac{1}{2},+∞)$.
综上所述,m=4时,f(x)的在定义域(0,+∞)单调递减;
当2<m<4时,函数f(x)的单调递增区间为$(\frac{1}{2},-\frac{1}{2-m})$,递减区间为$(0,\frac{1}{2})$,$(-\frac{1}{2-m},+∞)$;
当m>4时,函数f(x)的单调递增区间为$(-\frac{1}{2-m},\frac{1}{2})$,递减区间为$(0,-\frac{1}{2-m})$,$(\frac{1}{2},+∞)$.
(2)由(1)得:m∈(4,6)时,函数f(x)在[1,3]递减,
∴x∈[1,3]时,f(x)max=f(1)=5-2m,f(x)min=f(3)=mln3+$\frac{1}{3}$+12-6m,
问题等价于:对任意的m∈(4,6),恒有(a+ln3)(2-m)-2ln3>5-2m-mln3-$\frac{1}{3}$-12+6m成立,
即(2-m)a>$\frac{2}{3}$-4(2-m),
∵m>2,则a<$\frac{2}{3(2-m)}$-4,
∴a<${(\frac{2}{3(2-m)}-4)}_{min}$,
设m∈[4,6),则m=4时,$\frac{2}{3(2-m)}$-4取得最小值-$\frac{13}{3}$,
故a的范围是(-∞,-$\frac{13}{3}$].
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及函数恒成立问题,考查分类讨论思想,是一道综合题.


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{3}$ | B. | $\frac{10}{3}$ | C. | $\frac{3}{2}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 设函数f(x)=$\frac{b\sqrt{{a}^{2}-{x}^{2}}}{a}$(a>b>0)的图象是曲线C.
设函数f(x)=$\frac{b\sqrt{{a}^{2}-{x}^{2}}}{a}$(a>b>0)的图象是曲线C.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
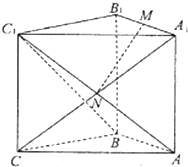 直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=BB1,M为A1B1的中点,N是AC1与A1C的交点.
直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=BB1,M为A1B1的中点,N是AC1与A1C的交点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
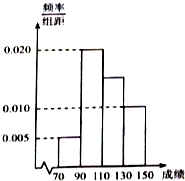 某班一次数学考试成绩频率分布直方图如图所示,数据分组依次为[70,90),[90,110),[110,130),[130,150],已知成绩大于等于90分的人数为36人,现采用分层抽样的方式抽取一个容量为10的样本.
某班一次数学考试成绩频率分布直方图如图所示,数据分组依次为[70,90),[90,110),[110,130),[130,150],已知成绩大于等于90分的人数为36人,现采用分层抽样的方式抽取一个容量为10的样本.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,已知圆内接四边形ABCD,记T=tan$\frac{A}{2}$+tan$\frac{B}{2}$+tan$\frac{C}{2}$+tan$\frac{D}{2}$.
如图所示,已知圆内接四边形ABCD,记T=tan$\frac{A}{2}$+tan$\frac{B}{2}$+tan$\frac{C}{2}$+tan$\frac{D}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com