
分析 在△ABC中由余弦定理求出cos∠BAC,由内角的范围和平方关系求出sin∠BAC,根据“∠DAC=∠BAC-∠BAD”和两角差的余弦公式求出cos∠DAC,由平方关系求出sin∠DAC,由商的关系表示出tan∠DAC,利用完全平方和公式和分母有理化进行化简即可.
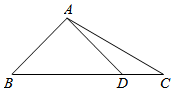
解答 解:在△ABC中,AB=2,AC=3,BC=4,
则由余弦定理得,cos∠BAC=$\frac{A{B}^{2}+A{C}^{2}-B{C}^{2}}{2•AB•AC}$=$\frac{4+9-16}{2×2×3}$=$-\frac{1}{4}$,
∵0<∠BAC<180°,
∴sin∠BAC=$\sqrt{1-co{s}^{2}∠BAC}$=$\frac{\sqrt{15}}{4}$,
由∠BAD=45°得,cos∠DAC=cos(∠BAC-∠BAD)
=cos(∠BAC-45°)=cos∠BACcos45°+sin∠BACsin45°
=$\frac{\sqrt{2}}{2}$(cos∠BAC+sin∠BAC)=$\frac{\sqrt{2}}{2}$($-\frac{1}{4}$+$\frac{\sqrt{15}}{4}$)=$\frac{\sqrt{2}(\sqrt{15}-1)}{8}$,
∴sin∠DAC=$\sqrt{1-co{s}^{2}∠DAC}$=$\frac{\sqrt{8+\sqrt{15}}}{4}$
∴tan∠DAC=$\frac{sin∠DAC}{cos∠DAC}$=$\frac{\sqrt{8+\sqrt{15}}}{4}×\frac{8}{\sqrt{2}(\sqrt{15}-1)}$=$\frac{\sqrt{2}•\sqrt{8+\sqrt{15}}}{\sqrt{15}-1}$
=$\frac{\sqrt{2}•\sqrt{8+\sqrt{15}}•(\sqrt{15}+1)}{14}$=$\frac{\sqrt{2}•\sqrt{(8+\sqrt{15})•(\sqrt{15}+1)^{2}}}{14}$
=$\frac{\sqrt{2}•\sqrt{158+32\sqrt{15}}}{14}$=$\frac{\sqrt{79+16\sqrt{15}}}{7}$
=$\frac{\sqrt{64+2×8×\sqrt{15}+(\sqrt{15})^{2}}}{7}$=$\frac{8+\sqrt{15}}{7}$.
点评 本题考查余弦定理,同角三角函数的基本关系,以及两角差的余弦公式,考查化简、变形能力.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | ln(ln2) | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,斜三棱柱ABC-A1B1C1,面AA1B1B⊥面ABC,且∠A1AB=60°,AA1=2,△ABC为边长为2的等边三角形,G为△ABC的重心,取BC中点F,连接B1F与BC1交于E点:
如图,斜三棱柱ABC-A1B1C1,面AA1B1B⊥面ABC,且∠A1AB=60°,AA1=2,△ABC为边长为2的等边三角形,G为△ABC的重心,取BC中点F,连接B1F与BC1交于E点:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,0) | B. | (0,-1) | C. | (0,1) | D. | (-1,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com