观察下列等式1=12+3+4=93+4+5+6+7=254+5+6+7+8+9+10=49--照此规律.第个等式为 . 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

观察下列等式
1=1
2+3+4=9
3+4+5+6+7=25
4+5+6+7+8+9+10=49
……
照此规律，第个等式为 .

解析

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：填空题

在平面上，我们用一直线去截正方形的一个角，那么截下的一个直角三角形，按如图所标边长，由勾股定理有．设想正方形换成正方体，把截线换成如图截面，这时从正方体上截下三条侧棱两两垂直的三棱锥，如果用表示三个侧面面积，表示截面面积，那么类比得到的结论是．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

观察下列等式

照此规律，第个等式为．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

若三角形内切圆的半径为r，三边长为，则三角形的面积，根据类比思想，若四面体内切球半径为R，四个面的面积为S₁_、S₂_、S₃_、S₄，则四面体的体积V= .

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

下面几种推理是合情推理的是。（填序号）
①由圆的性质类比出球的性质；
②由直角三角形、等腰三角形、等边三角形的内角和是180⁰，归纳得出所有三角形的内角和为180⁰；
③小王某次考试成绩是100分，由此推出全班同学的成绩都是100分；
④三角形的内角和是180⁰，四边形内角和是360⁰，五边形的内角和是540⁰，由此得凸n边形的内角和是.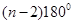

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

将长度为的线段分成段，每段长度均为正整数，并要求这段中的任意三段都不能构成三角形．例如，当时，只可以分为长度分别为1,1,2的三段，此时的最大值为3；当时，可以分为长度分别为1,2,4的三段或长度分别为1,1,2,3的四段，此时的最大值为4．则：
（1）当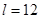时，的最大值为________；（2）当时，的最大值为________．