
分析 (1)根据直线分圆分成长度相等的四段弧,得到$|{AB}|=|{CD}|=\sqrt{2}$,利用点到直线的距离公式进行求解即可.
(2)根据直线与圆相交的位置关系,利用消元法转化为一元二次方程,根据根与系数之间的关系进行证明即可,
(3)根据椭圆内接正方形的关系,转化为一元二次方程,根据根与系数之间的关系进行证明即可,
解答 解:(1)由于直线l1:y=x+a和l2:y=x+b将单位圆W:x2+y2=(1分)成长度相等的四段弧,
所以$|{AB}|=|{CD}|=\sqrt{2}$,
在等腰直角△OAB中,圆心O(0,0)到直线l1:y=x+a的距离为$d=\frac{|a|}{{\sqrt{2}}}=\frac{{\sqrt{2}}}{2}∴|a|=1$,
同理|b|=1,∴a2+b2=2------------------------------------(4分)
(2)由题知,直线l1,l2关于原点对称,因为圆W:x2+y2=4的圆心为原点O,
所以$\overrightarrow{AB}=\overrightarrow{DC}$,故四边形ABCD为平行四边形.易知,O点在对角线AC,BD上.
联立$\left\{\begin{array}{l}{x^2}+{y^2}=4\\ y=2x-\sqrt{10}\end{array}\right.$解得$5{x^2}-4\sqrt{10}x+6=0$,由${x_1}+{x_2}=\frac{{4\sqrt{10}}}{5},{x_1}{x_2}=\frac{6}{5}$
得$\overrightarrow{OA}•\overrightarrow{OB}={x_1}{x_2}+{y_1}{y_2}={x_1}{x_2}+({2{x_1}-\sqrt{10}})({2{x_2}-\sqrt{10}})$=$5{x_1}{x_2}-2\sqrt{10}({{x_1}+{x_2}})+10=6-2\sqrt{10}•\frac{{4\sqrt{10}}}{5}+10=0$,
所以$\overrightarrow{OA}⊥\overrightarrow{OB}$,
于是$\overrightarrow{AC}⊥\overrightarrow{BD}$,因为$|{\overrightarrow{AC}}|=|{\overrightarrow{BD}}|=4$,所以四边形ABCD为正方形.----------------(9分)
(3)证明:假设椭圆$W:\frac{x^2}{2}+{y^2}=1$存在内接正方形,其四个顶点为A,B,C,D.
当直线AB的斜率不存在时,设直线AB、CD的方程为x=m,x=n,因为A,B,C,D在椭圆上,
所以$A({m,-\sqrt{1-\frac{m^2}{2}}}),B({m,\sqrt{1-\frac{m^2}{2}}}),C({n,-\sqrt{1-\frac{n^2}{2}}}),D({n,-\sqrt{1-\frac{n^2}{2}}})$,
由四边形ABCD为正方形,易知,$m=\frac{{\sqrt{6}}}{3},n=-\frac{{\sqrt{6}}}{3}$,直线AB、CD的方程为$x=\frac{{\sqrt{6}}}{3},x=-\frac{{\sqrt{6}}}{3}$,
正方形ABCD的面积$S=\frac{{2\sqrt{6}}}{3}•\frac{{2\sqrt{6}}}{3}=\frac{8}{3}$.---------------------(12分)
当直线AB的斜率存在时,设直线AB、CD的方程分别为lAB:y=kx+m,lCD:y=kx+n(k≠0,m≠0),
显然m≠n.设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),
联立$\left\{\begin{array}{l}\frac{x^2}{2}+{y^2}=1\\ y=kx+m\end{array}\right.$得(1+2k2)x2+4kmx+2m2-2=0,所以${x_1}+{x_2}=-\frac{4km}{{1+2{k^2}}},{x_1}{x_2}=\frac{{2{m^2}-2}}{{1+2{k^2}}}$
代人${|{AB}|^2}=({1+{k^2}})[{{{({{x_1}+{x_2}})}^2}-4{x_1}{x_2}}]$,得${|{AB}|^2}=8({1+{k^2}})•\frac{{2{k^2}-{m^2}+1}}{{{{({1+2{k^2}})}^2}}}$,
同理可得${|{CD}|^2}=8({1+{k^2}})•\frac{{2{k^2}-{n^2}+1}}{{{{({1+2{k^2}})}^2}}}$,
因为ABCD为正方形,所以|AB|2=|CD|2解得m2=n2
因为m≠n,所以m=-n,
因此,直线AB与直线CD关于原点O对称,
所以原点O为正方形的中心(由m=-n知$\overrightarrow{AB}=\overrightarrow{DC}$,四边形ABCD为平行四边形)
由ABCD为正方形知$\overrightarrow{OA}⊥\overrightarrow{OB}$,
即$\overrightarrow{OA}•\overrightarrow{OB}={x_1}{x_2}+{y_1}{y_2}=({1+{k^2}}){x_1}{x_2}+km({{x_1}+{x_2}})+{m^2}=0$
代人得$\frac{{3{m^2}-2{k^2}-2}}{{1+2{k^2}}}=0$,解得${m^2}=\frac{{2({{k^2}+1})}}{3}$(注:此时四边形ABCD为菱形)
由ABCD为正方形知|AB|=|AD|,
因为直线AB与直线CD的距离为$|{AD}|=\frac{{|{m-n}|}}{{\sqrt{1+{k^2}}}},m=-n$,故${|{AD}|^2}=\frac{{4{m^2}}}{{1+{k^2}}}=\frac{{4•\frac{{2({{k^2}+1})}}{3}}}{{1+{k^2}}}=\frac{8}{3}$
但${|{AB}|^2}=8({1+{k^2}})•\frac{{2{k^2}-{m^2}+1}}{{{{({1+2{k^2}})}^2}}}=\frac{8}{3}•\frac{{({1+{k^2}})({1+4{k^2}})}}{{{{({1+2{k^2}})}^2}}}$,
由$\frac{{({1+{k^2}})({1+4{k^2}})}}{{{{({1+2{k^2}})}^2}}}=1$得4k4+5k2+1=4k4+4k2+1,
∴k2=0即k=0,与k≠0矛盾.
所以|AD|2≠|AB|2,这与|AD|=|AB|矛盾.
即当直线AB的斜率k≠0存在时,椭圆内不存在正方形.
综上所述,椭圆$W:\frac{x^2}{2}+{y^2}=1$的内接正方形有且只有一个,且其面积为$S=\frac{8}{3}$.--(18分)
点评 本题主要考查直线和圆锥曲线的位置关系的应用,将直线方程代入椭圆方程,利用消元法转化为一元二次方程形式,根据根与系数之间的关系是解决本题的关键.综合性较强,难度较大.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 15 | C. | 35 | D. | 75 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
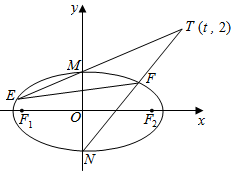 已知椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的上顶点M与左、右焦点F1,F2构成三角形MF1F2面积为$\sqrt{3}$,又椭圆C的离心率为$\frac{{\sqrt{3}}}{2}$.
已知椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的上顶点M与左、右焦点F1,F2构成三角形MF1F2面积为$\sqrt{3}$,又椭圆C的离心率为$\frac{{\sqrt{3}}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | -$\frac{3}{2}$ | C. | ±$\frac{3}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{15}}{10}$ | B. | $\frac{4\sqrt{15}}{15}$ | C. | $\frac{\sqrt{15}}{15}$ | D. | $\frac{2\sqrt{15}}{15}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com