[题目]解关于的不等式: . 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】解关于的不等式： .

【答案】见解析

【解析】试题分析：讨论a=0、a＞0和a＜0时，分别求出对应不等式的解集即可．

详解：不等式ax2+（2﹣a）x﹣2＞0化为（ax+2）（x﹣1）＞0，

当a=0时，不等式化为x﹣1＞0，

解得x＞1；

当a＞0时，不等式化为（x+）（x﹣1）＞0，

且﹣＜1，解不等式得x＜﹣或x＞1；

当a＜0时，不等式化为（x+）（x﹣1）＜0，

若a＜﹣2，则﹣＜1，解不等式得﹣＜x＜1；

若a=﹣2，则﹣=1，不等式化为（x﹣1）2＜0，解得x∈；

若﹣2＜a＜0，则﹣＞1，解不等式得1＜x＜﹣；

综上，a=0时不等式的解集为{x|x＞1}；

a＞0时不等式的解集为{x|x＜﹣或x＞1}；

a＜﹣2时，不等式的解集为{x|﹣＜x＜1}；

a=﹣2时，不等式的解集为；

﹣2＜a＜0时，不等式的解集为{x|1＜x＜﹣}．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

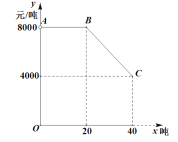
【题目】乔经理到老陈的果园里一次性采购一种水果，他俩商定：乔经理的采购价（元/吨）与采购量（吨）之间函数关系的图像如图中的折线段所示（不包含端点但包含端点）.

（1）求与之间的函数关系式；

（2）已知老陈种植水果的成本是2800元/吨，那么乔经理的采购量为多少时，老陈在这次买卖中所获的利润最大？最大利润是多少？

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】下列命题错误的是（）
A.命题“若，则 ”的逆命题为“若，则 ”
B.对于命题，使得，则，则
C.“ ”是“ ”的充分不必要条件
D.若为假命题，则均为假命题

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某市电视台为了提高收视率而举办有奖问答活动，随机对该市15～65岁的人群抽样了人，回答问题统计结果及频率分布直方图如图表所示.

（1）分别求出的值；
（2）从第2，3，4组回答正确的人中用分层抽样的方法抽取6人，则第2，3，4组每组应各抽取多少人？
（3）在（2）的前提下，电视台决定在所抽取的6人中随机抽取2人颁发幸运奖，求所抽取的人中第2组至少有1人获得幸运奖的概率.