
【题目】设函数![]() .
.
(1)讨论![]() 的极值点;
的极值点;
(2)若有最大值![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(1)![]() 时,无极值点,
时,无极值点,![]() 时,
时,![]() 为极大值点,无极小值点;(2)
为极大值点,无极小值点;(2)![]()
【解析】
(1)函数f(x)的定义域为(0,+∞),对f(x)求导![]() ,对
,对![]() 分类讨论即可得出.
分类讨论即可得出.
(2)由(1)利用单调性先得到![]() 与b的关系,代入所求,构造函数求导即可得出.
与b的关系,代入所求,构造函数求导即可得出.
(1)函数f(x)的定义域为(0,+∞),![]() ,
,
当a≤0时,f'(x)>0,∴f(x)在(0,+∞)上单调递增,无极值点;
当a>0时,解f'(x)>0得![]() ,
,
∴f(x)在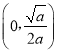 上单调递增,在
上单调递增,在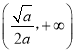 上单调递减,所以
上单调递减,所以![]() 为极大值点,无极小值点;
为极大值点,无极小值点;
(2)由(1)知,当a>0时,f(x)在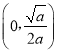 上单调递增,在
上单调递增,在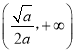 上单调递减.
上单调递减.
∴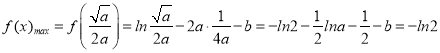 ,
,
∴![]() ,∴
,∴![]() ,
,
令![]() ,则
,则![]() ,
,
∴h(a)在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
∴![]() ,∴a+2b的最小值为
,∴a+2b的最小值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知直线![]() :
: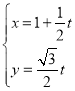 (
(![]() 为参数),曲线
为参数),曲线![]() :
:![]() (
(![]() 为参数).
为参数).
(1)设![]() 与
与![]() 相交于
相交于![]() 两点,求
两点,求![]() ;
;
(2)若把曲线![]() 上各点的横坐标压缩为原来的
上各点的横坐标压缩为原来的![]() 倍,纵坐标压缩为原来的
倍,纵坐标压缩为原来的![]() 倍,得到曲线
倍,得到曲线![]() ,设点P是曲线
,设点P是曲线![]() 上的一个动点,求它到直线
上的一个动点,求它到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以原点为极点,
为参数),以原点为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为:
的极坐标方程为:![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)写出曲线![]() 的极坐标方程,并指出它是何种曲线;
的极坐标方程,并指出它是何种曲线;
(Ⅱ)设![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,求四边形
两点,求四边形![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“干支纪年法”是中国历法上自古以来使用的纪年方法,甲、乙、丙、丁、戊、己、庚、辛、壬、癸被称为“十天干”,子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥叫做“十二地支”。“天干”以“甲”字开始,“地支”以“子”字开始,两者按干支顺序相配,组成了干支纪年法,其相配顺序为:甲子、乙丑、丙寅…癸酉,甲戌、乙亥、丙子…癸末,甲申、乙酉、丙戌…癸巳,…,共得到![]() 个组成,周而复始,循环记录。2014年是“干支纪年法”中的甲午年,那么2020年是“干支纪年法”中的()
个组成,周而复始,循环记录。2014年是“干支纪年法”中的甲午年,那么2020年是“干支纪年法”中的()
A. 己亥年 B. 戊戌年 C. 庚子年 D. 辛丑年
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十二生肖,又称十二属相,中国古人拿十二种动物来配十二地支,组成子鼠、丑牛、寅虎、卯兔、辰龙、巳蛇、午马、未羊、申猴、酉鸡、戌狗、亥猪十二属相。现有十二生肖吉祥物各一件,甲、乙、丙三位同学一次随机抽取一件作为礼物,甲同学喜欢马、牛,乙同学喜欢马、龙、狗,丙同学除了鼠不喜欢外其他的都喜欢,则这三位同学抽取的礼物都喜欢的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)="xln" x–ax2+(2a–1)x,a![]() R.
R.
(Ⅰ)令g(x)=f'(x),求g(x)的单调区间;
(Ⅱ)已知f(x)在x=1处取得极大值.求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况. 下列叙述中正确的是( )

A. 消耗1升汽油,乙车最多可行驶5千米
B. 以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多
C. 甲车以80千米/小时的速度行驶1小时,消耗10升汽油
D. 某城市机动车最高限速80千米/小时. 相同条件下,在该市用丙车比用乙车更省油
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com