
【题目】在直角坐标系中,已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以原点为极点,
为参数),以原点为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为:
的极坐标方程为:![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)写出曲线![]() 的极坐标方程,并指出它是何种曲线;
的极坐标方程,并指出它是何种曲线;
(Ⅱ)设![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,求四边形
两点,求四边形![]() 面积的取值范围.
面积的取值范围.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() 在
在![]() 处的切线
处的切线![]() 与直线
与直线![]() 平行.
平行.
(1)求实数![]() 的值;
的值;
(2)若函数![]() 在
在![]() 上恰有两个零点,求实数
上恰有两个零点,求实数![]() 的取值范围.
的取值范围.
(3)记函数![]() ,设
,设![]() 是函数
是函数![]() 的两个极值点,若
的两个极值点,若![]() ,且
,且![]() 恒成立,求实数
恒成立,求实数![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某周末,郑州方特梦幻王国汇聚了八方来客.面对该园区内相邻的两个主题公园“千古蝶恋”和“西游传说”,成年人和未成年人选择游玩的意向会有所不同.某统计机构对园区内的100位游客(这些游客只在两个主题公园中二选一)进行了问卷调查.调查结果显示,在被调查的50位成年人中,只有10人选择“西游传说”,而选择“西游传说”的未成年人有20人.
(1)根据题意,请将下面的![]() 列联表填写完整;
列联表填写完整;
选择“西游传说” | 选择“千古蝶恋” | 总计 | |
成年人 | |||
未成年人 | |||
总计 |
(2)根据列联表的数据,判断是否有![]() 的把握认为选择哪个主题公园与年龄有关.
的把握认为选择哪个主题公园与年龄有关.
附参考公式与表: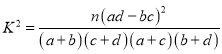 (
(![]() ).
).
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的一个顶点为抛物线
的一个顶点为抛物线![]() 的焦点,点
的焦点,点![]() 在椭圆
在椭圆![]() 上且
上且![]() ,
,![]() 关于原点
关于原点![]() 的对称点为
的对称点为![]() ,过
,过![]() 作
作![]() 的垂线交椭圆于另一点
的垂线交椭圆于另一点![]() ,连
,连![]() 交
交![]() 轴于
轴于![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)求证:![]() 轴;
轴;
(3)记![]() 的面积为
的面积为![]() 的面积为
的面积为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过去大多数人采用储蓄的方式将钱储蓄起来,以保证自己生活的稳定,考虑到通货膨胀的压力,如果我们把所有的钱都用来储蓄,这并不是一种很好的方式,随着金融业的发展,普通人能够使用的投资理财工具也多了起来,为了研究某种理财工具的使用情况,现对![]() 年龄段的人员进行了调查研究,将各年龄段人数分成5组:
年龄段的人员进行了调查研究,将各年龄段人数分成5组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,并整理得到频率分布直方图:
,并整理得到频率分布直方图:
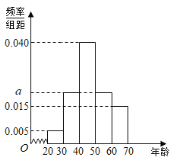
(1)求图中的a值;
(2)采用分层抽样的方法,从第二组、第三组、第四组中共抽取8人,则三个组中,各抽取多少人;
(3)由频率分布直方图,求所有被调查人员的平均年龄.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]()
![]() 的一个焦点为
的一个焦点为![]() ,且椭圆
,且椭圆![]() 过点
过点![]() ,
,![]() 为坐标原点,
为坐标原点,
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆![]() 恒有两个交点
恒有两个交点![]() 、
、![]() ,且
,且![]() ?若存在,写出该圆的方程,并求
?若存在,写出该圆的方程,并求![]() 的最大值,若不存在说明理由.
的最大值,若不存在说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com