Question

3．已知实数x，y满足可行域$D：\left\{\begin{array}{l}x+2y-4≤0\\ 3x-2y+6≥0\\ y≥0\end{array}\right.$，曲线C：|x|+|y|-a=0恰好平分可行域D的面积，则a的值为（　　）

• A． 2
• B． $\frac{{3\sqrt{2}}}{2}$
• C． $\frac{{\sqrt{6}}}{2}$
• D． $\frac{{3\sqrt{6}}}{4}$

Answer 1

分析 作出不等式组对应的平面区域，确定x，y的取值范围将曲线进行化简，利用面积关系进行转化求即可即可．

解答 解：作出不等式组对应的平面区域如图：则B（-2，0），C（4，0），
由$\left\{\begin{array}{l}{x+2y-4=0}\\{3x-2y+6=0}\end{array}\right.$，解得$\left\{\begin{array}{l}{x=-\frac{1}{2}}\\{y=\frac{9}{4}}\end{array}\right.$，即A（$-\frac{1}{2}$，$\frac{9}{4}$），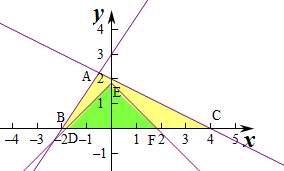
则y≥0且-2≤x≤4，
则曲线T：|x|+|y|-a=0，等价为|x|-y-a=0，即y=a-|x|，
△ABC的面积S=$\frac{1}{2}×6×\frac{9}{4}$=$\frac{27}{4}$，
作出直线y=a-|x|的图象如图，
则对应的区域为△DEF，
其中E（0，a），D（-a，0），F（a，0），则△DEF的面积S=$\frac{1}{2}×2a•a$=a²=$\frac{1}{2}$×$\frac{27}{4}$=$\frac{27}{8}$，
则a=$\sqrt{\frac{27}{8}}$=$\frac{{3\sqrt{6}}}{4}$，
故选：D．

点评 本题主要考查线性规划的应用，根据图象将曲线进行化简是解决本题的关键，考查学生的运算和推理能力．