
【题目】已知函数f(x)=![]() 是定义在R上的奇函数;
是定义在R上的奇函数;
(1)求a、b的值,判断并证明函数y=f(x)在区间(1,+∞)上的单调性
(2)已知k<0且不等式f(t2-2t+3)+f(k-1)<0对任意的t∈R恒成立,求实数k的取值范围.
【答案】(1)见解析(2)(-1,0)
【解析】
(1)根据奇函数的定义即可求出a、b的值,再根据增减性定义证明函数单调性即可
(2)根据奇函数的性质及函数的增减性原不等式可转化为t2-2t+3>1-k对任意的t∈R恒成立,只需求出t2-2t+3的最小值即可.
(1)∵函数f(x)=![]() 是奇函数
是奇函数
∴由定义f(-x)=![]() =-
=-![]() ,
,
∴a=b=0,
∴f(x)=![]() ,
,
y=f(x)在区间(1,+∞)上的单调递减.
证明如下:
∵f(x)=![]() ,∴
,∴![]() ,
,
∵x>1,∴![]() ,
,
∴y=f(x)在区间(1,+∞)上的单调递减.
(2)由f(t2-2t+3)+f(k-1)<0及f(x)为奇函数得:f(t2-2t+3)<f(1-k)
因为t2-2t+3≥2,1-k>1,且y=f(x)在区间(1,+∞)上的单调递减,
所以t2-2t+3>1-k任意的t∈R恒成立,
因为t2-2t+3的最小值为2,所以2>1-k,∴k>-1
∵k<0,∴-1<k<0.
∴实数k的取值范围是(-1,0).


科目:高中数学 来源: 题型:
【题目】在篮球比赛中,如果某位球员的得分,篮板,助攻,抢断,盖帽中有两个值达到![]() 或
或![]() 以上,就称该球员拿到了两双.下表是某球员在最近五场比赛中的数据统计:
以上,就称该球员拿到了两双.下表是某球员在最近五场比赛中的数据统计:
场次 | 得分 | 篮板 | 助攻 | 抢断 | 盖帽 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(![]() )从上述比赛中任选
)从上述比赛中任选![]() 场,求该球员拿到“两双”的概率.
场,求该球员拿到“两双”的概率.
(![]() )从上述比赛中任选
)从上述比赛中任选![]() 场,设该球员拿到“两双”的次数为
场,设该球员拿到“两双”的次数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
(![]() )假设各场比赛互相独立,将该球员在上述比赛中获得“两双”的频率作为概率,设其在接下来的三场比赛中获得“两双”的次数为
)假设各场比赛互相独立,将该球员在上述比赛中获得“两双”的频率作为概率,设其在接下来的三场比赛中获得“两双”的次数为![]() ,试比赛
,试比赛![]() 与
与![]() 的大小关系(只需写出结论).
的大小关系(只需写出结论).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,已知圆C的圆心C( ![]() ,
, ![]() ),半径r=
),半径r= ![]() .
.
(1)求圆C的极坐标方程;
(2)若α∈[0, ![]() ),直线l的参数方程为
),直线l的参数方程为 ![]() (t为参数),直线l交圆C于A、B两点,求弦长|AB|的取值范围.
(t为参数),直线l交圆C于A、B两点,求弦长|AB|的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数g(x)=ax2-2ax+1+b(a>0)在区间[2,4]上的最大值为9,最小值为1,记f(x)=g(|x|).
(1)求实数a,b的值;
(2)若不等式f(log2k)>f(2)成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学进行自主招生时,需要进行逻辑思维和阅读表达两项能力的测试.学校对参加测试的200名学生的逻辑思维成绩、阅读表达成绩以及这两项的总成绩进行了排名.其中甲、乙、丙三位同学的排名情况如下图所示:
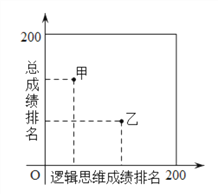

得出下面四个结论:
①甲同学的阅读表达成绩排名比他的逻辑思维成绩排名更靠前
②乙同学的逻辑思维成绩排名比他的阅读表达成绩排名更靠前
③甲、乙、丙三位同学的逻辑思维成绩排名中,甲同学更靠前
④乙同学的总成绩排名比丙同学的总成绩排名更靠前
则所有正确结论的序号是_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|1≤x≤3},B={x|x>2}.
(Ⅰ)分别求A∩B,(RB)∪A;
(Ⅱ)已知集合C={x|1<x<a},若CA,求实数a的取值集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣1|+|x+a|,其中a为实常数.
(1)若函数f(x)的最小值为2,求a的值;
(2)当x∈[0,1]时,不等式|x﹣2|≥f(x)恒成立,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com