
分析 由函数的周期性可得f(-2)=f(2),f(1)=f(-1),可得m和n的方程组,解方程组求解定积分可得.
解答 解:∵f(x)是定义在R上且周期为4的函数,在区间[-2,2]上
有$f(x)=\left\{\begin{array}{l}mx+2,-2≤x<0\\ \frac{nx-2}{x+1},0≤x≤2\end{array}\right.$,且f(1)=f(3),
∴f(-2)=f(2),f(1)=f(3)=f(-1),
∴-2m+2=$\frac{2n-2}{3}$,$\frac{n-2}{2}$=-m+2,
联立解得m=-2,n=10,
∴$\frac{1}{4}\int_{-1}^3{(mx+n})dx$=$\frac{1}{4}$•($\frac{1}{2}$mx2+nx)${|}_{-1}^{3}$=m+n=8
故答案为:8
点评 本题考查定积分的求解,涉及分段函数以及函数的周期性,属中档题.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源: 题型:解答题
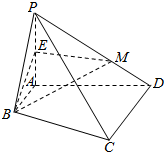 如图,在四棱锥P-ABCD中,平面PAB⊥平面ABCD,AB∥CD,AB⊥AD,CD=2AB,E为PA的中点,M在PD上.
如图,在四棱锥P-ABCD中,平面PAB⊥平面ABCD,AB∥CD,AB⊥AD,CD=2AB,E为PA的中点,M在PD上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 0 | 1 | 2 | 3 |
| y | 3 | 3.5 | 4.5 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -24 | B. | -17 | C. | -3 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com