
���� ���������ֱ���$\overrightarrow{OA}=\overrightarrow{a}$��$\overrightarrow{OB}=\overrightarrow{b}$��$\overrightarrow{OC}=\overrightarrow{c}$������AB��AC��BC����ɵõ�$��AOB=\frac{��}{3}$��$��ACB=\frac{2��}{3}$��$|\overrightarrow{AC}|=2\sqrt{3}$��$|\overrightarrow{AB}|=5$���Ӷ�˵��A��O��B��C�ĵ㹲Բ������С�ABC=��AOC��������������֪��ABCΪ��ֵ���������Ҷ����ɵõ�sin��ABC=$\frac{3}{5}$��cos$��ABC=\frac{4}{5}$�����õ�cos��AOC=$\frac{4}{5}$���������֪��ֻҪ$|\overrightarrow{a}||\overrightarrow{c}|$ȡ�����ֵ��������$|\overrightarrow{c}-\overrightarrow{a}|=2\sqrt{3}$��õ�$12={\overrightarrow{c}}^{2}+{\overrightarrow{a}}^{2}-\frac{8}{5}|\overrightarrow{c}||\overrightarrow{a}|$���ɲ���ʽ${\overrightarrow{c}}^{2}+{\overrightarrow{a}}^{2}��2|\overrightarrow{a}||\overrightarrow{c}|$�������$|\overrightarrow{a}||\overrightarrow{c}|$�����ֵ���Ӷ��ó�$\overrightarrow{a}•\overrightarrow{c}$�����ֵ��
���  �⣺��ͼ����$\overrightarrow{OA}=\overrightarrow{a}$��$\overrightarrow{OB}=\overrightarrow{b}$����$��AOB=\frac{��}{3}$����$\overrightarrow{OC}=\overrightarrow{c}$����$\overrightarrow{AC}=\overrightarrow{c}-\overrightarrow{a}��\overrightarrow{BC}=\overrightarrow{c}-\overrightarrow{b}$����$��ACB=\frac{2��}{3}$���Ӷ�A��O��B��C�ĵ㹲Բ��
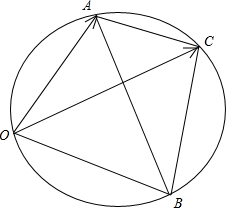
�⣺��ͼ����$\overrightarrow{OA}=\overrightarrow{a}$��$\overrightarrow{OB}=\overrightarrow{b}$����$��AOB=\frac{��}{3}$����$\overrightarrow{OC}=\overrightarrow{c}$����$\overrightarrow{AC}=\overrightarrow{c}-\overrightarrow{a}��\overrightarrow{BC}=\overrightarrow{c}-\overrightarrow{b}$����$��ACB=\frac{2��}{3}$���Ӷ�A��O��B��C�ĵ㹲Բ��
���AOC=��ABC��
�ڡ�ABC�У�$|\overrightarrow{AC}|=|\overrightarrow{c}-\overrightarrow{a}|=2\sqrt{3}$��|$\overrightarrow{AB}$|=$|\overrightarrow{b}-\overrightarrow{a}|=5$��$��ACB=\frac{2��}{3}$��
�����Ҷ����ã�$\frac{|\overrightarrow{AC}|}{sin��ABC}=\frac{|\overrightarrow{AB}|}{sin��ACB}$��
��$\frac{2\sqrt{3}}{sin��ABC}=\frac{5}{sin\frac{2��}{3}}$��
��sin��ABC=$\frac{3}{5}$��
��$cos��ABC=\frac{4}{5}$��
��$cos��AOC=\frac{4}{5}$��
��$|\overrightarrow{c}-\overrightarrow{a}|=2\sqrt{3}$�ã�$12=|\overrightarrow{c}{|}^{2}+|\overrightarrow{a}{|}^{2}-2|\overrightarrow{c}||\overrightarrow{a}|•\frac{4}{5}$=$|\overrightarrow{c}{|}^{2}+|\overrightarrow{a}{|}^{2}-\frac{8}{5}|\overrightarrow{c}||\overrightarrow{a}|$$��2|\overrightarrow{c}||\overrightarrow{a}|-\frac{8}{5}|\overrightarrow{c}||\overrightarrow{a}|$=$\frac{2}{5}|\overrightarrow{c}||\overrightarrow{a}|$��
��$|\overrightarrow{c}||\overrightarrow{a}|��30$��
��$\overrightarrow{a}•\overrightarrow{c}=|\overrightarrow{a}||\overrightarrow{c}|•cos��AOC$=$\frac{4}{5}|\overrightarrow{a}||\overrightarrow{c}|��24$��
������$\overrightarrow{a}•\overrightarrow{c}$�����ֵΪ24��
�ʴ�Ϊ��24��
���� �������������ļ������壬�����нǵĸ���Լ��ĵ㹲Բ�ĸ���жϣ����Ҷ����������������ļ��㹫ʽ������ʽa2+b2��2ab������ֵʱ�����ã�


 ����ѧҵ���Ե�����ϵ�д�
����ѧҵ���Ե�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a=5 | B�� | a=3 | C�� | a��5 | D�� | a��-3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | n | B�� | n+1 | C�� | 2n | D�� | 2n-1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com