
现有一个关于平面图形的命题:如图所示,同一个平面内有两个边长都是 的正方形,其中一个的某顶点在另一个的中心,则这两个正方形重叠部分的面积恒为
的正方形,其中一个的某顶点在另一个的中心,则这两个正方形重叠部分的面积恒为 ;类比到空间,有两个棱长均为
;类比到空间,有两个棱长均为 的正方体,其中一个的某顶点在另一个的中心,则这两个正方体重叠部分的体积恒为 .
的正方体,其中一个的某顶点在另一个的中心,则这两个正方体重叠部分的体积恒为 .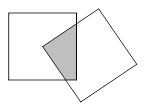
 优等生题库系列答案
优等生题库系列答案科目:高中数学 来源: 题型:填空题
1955年,印度数学家卡普耶卡(D.R.Kaprekar)研究了对四位自然数的一种交换:任给出四位数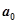 ,用
,用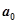 的四个数字由大到小重新排列成一个四位数m,再减去它的反序数n(即将
的四个数字由大到小重新排列成一个四位数m,再减去它的反序数n(即将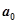 的四个数字由小到大排列,规定反序后若左边数字有0,则将0去掉运算,比如0001,计算时按1计算),得出数
的四个数字由小到大排列,规定反序后若左边数字有0,则将0去掉运算,比如0001,计算时按1计算),得出数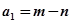 ,然后继续对
,然后继续对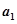 重复上述变换,得数
重复上述变换,得数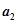 ,…,如此进行下去,卡普耶卡发现,无论
,…,如此进行下去,卡普耶卡发现,无论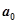 是多大的四位数,只要四个数字不全相同,最多进行k次上述变换,就会出现变换前后相同的四位数t(这个数称为Kaprekar变换的核).通过研究10进制四位数2014可得Kaprekar变换的核为 .
是多大的四位数,只要四个数字不全相同,最多进行k次上述变换,就会出现变换前后相同的四位数t(这个数称为Kaprekar变换的核).通过研究10进制四位数2014可得Kaprekar变换的核为 .
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
若等差数列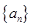 的首项为
的首项为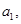 公差为
公差为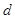 ,前
,前 项的和为
项的和为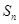 ,则数列
,则数列 为等差数列,且通项为
为等差数列,且通项为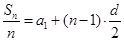 .类似地,请完成下列命题:若各项均为正数的等比数列
.类似地,请完成下列命题:若各项均为正数的等比数列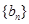 的首项为
的首项为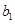 ,公比为
,公比为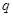 ,前
,前 项的积为
项的积为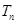 ,则 .
,则 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com