练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    17．已知5件产品中有2件次品，其余为合格品．现从这5件产品中任取2件，恰有一件次品的概率为$\frac{3}{5}$．

    分析 先求出基本事件总数，再求出恰有一件次品包含的基本事件个数，由此能求出恰有一件次品的概率．

    解答 解：5件产品中有2件次品，其余为合格品．现从这5件产品中任取2件，
    基本事件总数n=${C}_{5}^{2}$=10，
    恰有一件次品包含的基本事件个数m=${C}_{3}^{1}{C}_{2}^{1}=6$，
    ∴恰有一件次品的概率p=$\frac{m}{n}$=$\frac{6}{10}$=$\frac{3}{5}$．
    故答案为：$\frac{3}{5}$．

    点评 本题考概率的求法，是基础题，解题时要认真审题，注意等可能事件概率计算公式的合理运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    7．若复数z满足$\frac{z+i}{-2{i}^{3}-z}$=i，则|$\overline{z}$+1|=（　　）
    A．$\frac{1}{2}$B．$\frac{{\sqrt{2}}}{2}$C．$\frac{{\sqrt{3}}}{2}$D．1

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．下列说法正确的是（　　）
    A．|r|≤1；r越大，相关程度越大；反之，相关程度越小
    B．线性回归方程对应的直线$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$至少经过其样本数据点（x1，y1），（x2，y2），（x3，y3），（xn，yn）中的一个点
    C．在残差图中，残差点分布的带状区域的宽度越狭窄，其模型拟合的精度越高
    D．在回归分析中，相关指数R2为0.98的模型比相关指数R2为0.80的模型拟合的效果差

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．直线y+2=k （x+1）恒过点（　　）
    A．（2，1）B．（-2，-1）C．（-1，-2）D．（1，2）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．已知正方体的外接球的体积是$\frac{32}{3}$π，则这个正方体的体积是（　　）
    A．$\frac{64}{27}$B．$\frac{{64\sqrt{3}}}{9}$C．$\frac{64}{9}$D．$\frac{{64\sqrt{3}}}{27}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

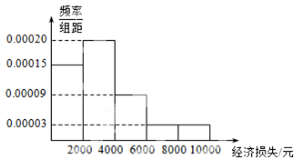    2．适逢暑假，小王在某小区调查了50户居民由于洪灾造成的经济损失，将收集的数据分成[0，2000]，（2000，4000]，（4000，6000]，（6000，8000]，（8000，10000]五组，并作出频率分布直方图（如图）．
    （Ⅰ）小王向班级同学发出为该小区居民捐款的倡议．若先从损失超过6000元的居民中随机抽出2户进行捐款援助，求这2户不在同一分组的概率；
    （Ⅱ）洪灾过后小区居委会号召小区居民为洪灾重灾区捐款，小王调查的50户居民的捐款情况如表，在表格空白处填写正确的数字，并说明是否有95%以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关？
    经济损失不超过4000元经济损失超过4000元合计
    捐款超过500元30939
    捐款不超过500元5611
    合计351550
    P（K2≥k0）0.150.100.050.0250.0100.0050.001
    k02.0722.7063.8415.0246.6357.87910.828
    参考公式：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$（其中n=a+b+c+d为样本容量）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．中国古代数学名著《张丘建算经》中记载：“今有马行转迟，次日减半，疾七日，行七百里．”意思是：现有一匹马行走的速度逐渐减慢，每天走的里程数是前一天的一半，连续行走7日，共走了700里．若该匹马连续按此规律行走，则它在第8天到第14天这7天时间所走的总里程为（　　）
    A．350里B．1050里C．$\frac{175}{32}$里D．.$\frac{22575}{32}$里

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．直线l过点P0（-4，0），它的参数方程为$\left\{\begin{array}{l}{x=-4+\frac{\sqrt{3}}{2}t}\\{y=\frac{1}{2}t}\end{array}\right.$（t为参数）与圆x2+y2=7相交于A，B两点，则弦长|AB|=2$\sqrt{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．若函数y=cos2x-asinx+b的最大值为0，最小值为-4，试求a与b的值，并求使y取得最大值和最小值时的x值．

    查看答案和解析>>

    同步练习册答案