
分析 求出p,q成立的等价条件,(Ⅰ)若“p∧q”为真命题,则p真q真,即可求实数m的取值范围;
(Ⅱ)若“p∧q”为假命题,“p∨q”为真命题,则p、q一真一假,当p真q假时,求出m的取值范围,当p假q真时,求出m的取值范围,然后取并集即可得答案.
解答 解:由2x-5>0,得$x>\frac{5}{2}$.
命题p真时,则($\frac{5}{2}$,+∞)?(m,+∞),得m$≤\frac{5}{2}$.
∴命题p假时,$m>\frac{5}{2}$.
命题q真时,得(m-1)(2-m)<0,解得m<1或m>2.
命题q假时,1≤m≤2.
(Ⅰ)若“p∧q”为真命题,则p真q真,
∴$\left\{\begin{array}{l}{m≤\frac{5}{2}}\\{m<1或m>2}\end{array}\right.$,解得m<1或$2<m≤\frac{5}{2}$.
∴实数m的取值范围为:(-∞,1)∪(2,$\frac{5}{2}$];
(Ⅱ)若“p∧q”为假命题,“p∨q”为真命题,则p、q一真一假,
当p真q假时,则$\left\{\begin{array}{l}{m≤\frac{5}{2}}\\{1≤m≤2}\end{array}\right.$,解得1≤m≤2.
当p假q真时,则$\left\{\begin{array}{l}{m>\frac{5}{2}}\\{m<1或m>2}\end{array}\right.$,解得$m>\frac{5}{2}$.
综上,实数m的取值范围为:[1,2]∪($\frac{5}{2}$,+∞).
点评 本题主要考查充分条件和必要条件的应用,利用双曲线方程的等价条件是解决本题的关键,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | (¬p)∨(¬q) | B. | p∨(¬q) | C. | (¬p)∧(¬q) | D. | p∨q |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (±$\sqrt{3}$,0) | B. | (0,±$\sqrt{3}$) | C. | (±3,0) | D. | (0,±3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在底面为平行四边形的四棱锥P-ABCD中,PA⊥平面ABCD,且BC=2AB═4,∠ABC=60°,点E是PD的中点.
如图,在底面为平行四边形的四棱锥P-ABCD中,PA⊥平面ABCD,且BC=2AB═4,∠ABC=60°,点E是PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 张邱建,北魏人,约公元5世纪,古代著名数学家,一生从事数学研究,造诣很深,其代表作《张邱建算经》采用问答式,调理精密,文词古雅,是世界数学资料库中的一份异常.其卷上第22题有一个“女子织布”问题:今有女善织,日益功疾,初日织五尺,今一月日织九匹三丈.问日益几何.”翻译过来的意思是意思是某女子善于织布,一天比一天织得快,而且每天增加的数量相同.已知第一天织布5尺,30天宫织布390尺,则该女子织布每天增加( )尺?
张邱建,北魏人,约公元5世纪,古代著名数学家,一生从事数学研究,造诣很深,其代表作《张邱建算经》采用问答式,调理精密,文词古雅,是世界数学资料库中的一份异常.其卷上第22题有一个“女子织布”问题:今有女善织,日益功疾,初日织五尺,今一月日织九匹三丈.问日益几何.”翻译过来的意思是意思是某女子善于织布,一天比一天织得快,而且每天增加的数量相同.已知第一天织布5尺,30天宫织布390尺,则该女子织布每天增加( )尺?| A. | $\frac{16}{29}$ | B. | $\frac{8}{15}$ | C. | $\frac{16}{31}$ | D. | $\frac{9}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
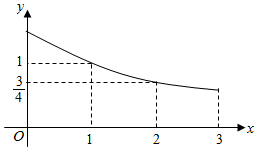 已知函数f(x)是定义在[-3,0)∪(0,3]上的奇函数,当x∈(0,3]时,f(x)的图象如图所示,那么满足不等式f(x)≥2x-1的取值范围是( )
已知函数f(x)是定义在[-3,0)∪(0,3]上的奇函数,当x∈(0,3]时,f(x)的图象如图所示,那么满足不等式f(x)≥2x-1的取值范围是( )| A. | [-2,1] | B. | [-3,-2]∪(0,3] | C. | [-2,0]∪(1,4] | D. | [-3,0]∪[2,5] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com