
(本题满分13分)
某俱乐部举行迎圣诞活动,每位会员交50元活动费,可享受20元的消费,并参加一次游戏:掷两颗正方体骰子,点数之和为12点获一等奖,奖价值为a元的奖品;点数之和为11或10点获二等奖,奖价值为100元的奖品;点数之和为9或8点获三等奖,奖价值为30元的奖品;点数之和小于8点的不得奖。求:
(1)同行的两位会员中一人获一等奖、一人获二等奖的概率;
(2)如该俱乐部在游戏环节不亏也不赢利,求a的值。
(1)P(A)=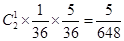 ; (2)一等奖可设价值为310 元的奖品。
; (2)一等奖可设价值为310 元的奖品。
解析试题分析:(Ⅰ)设掷两颗正方体骰子所得的点数记为(x,y),其中1≤x,y≤6,则获
一等奖只有(6,6)一种可能,获二等奖共有(6,5)、(5,6)、(4,6)、(6,4)、(5,5)共5种可能,由此能求出同行的三位会员一人获一等奖、两人获二等奖的概率.
(Ⅱ)设俱乐部在游戏环节收益为ξ元,则ξ的可能取值为30-a,-70,0,30,分别求
出P(ξ=30-a),P(ξ=-70),P(ξ=0),P(ξ=30)的值,由此能求出ξ的分布列和
Eξ.
解:(1)设掷两颗正方体骰子所得的点数记为(x,y),其中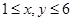 ,
,
则获一等奖只有(6,6)一种可能,其概率为: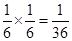 ; …………2分
; …………2分
获二等奖共有(6,5)、(5,6)、(4,6)、(6,4)、(5,5)共5种可能,其概率为: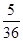 ;
;
…………5分
设事件A表示“同行的两位会员中一人获一等奖、一人获二等奖”,则有:
P(A)=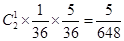 ; …………6分
; …………6分
(2)设俱乐部在游戏环节收益为ξ元,则ξ的可能取值为 ,
,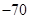 ,0,
,0,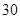 ,……7分
,……7分
其分布列为:ξ 30-a -70 0 30 p 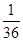
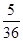
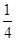
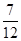
则:Eξ= ; …………11分
; …………11分
由Eξ=0得:a=310,即一等奖可设价值为310 元的奖品。 …………13分
考点:本试题主要考查了离散型随机变量的分布列和数学期望.
点评:解决该试题的关键是解题时要认真审题,理解古典概型的特征:试验结果的有限性和每一个试验结果出现的等可能性,体现了化归的重要思想.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:解答题
(本小题满分12分)电信公司进行促销活动,促销方案为顾客消费1000元,便可获得奖券一张,每张奖券中奖的概率为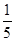 ,中奖后电信公司返还顾客现金1000元,小李购买一台价格2400元的手机,只能得2张奖券,于是小李补偿50元给同事购买一台价格600元的小灵通(可以得到三张奖券),小李抽奖后实际支出为X(元).
,中奖后电信公司返还顾客现金1000元,小李购买一台价格2400元的手机,只能得2张奖券,于是小李补偿50元给同事购买一台价格600元的小灵通(可以得到三张奖券),小李抽奖后实际支出为X(元).
(I)求X的分布列;(II)试说明小李出资50元增加1张奖券是否划算。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
公安部发布酒后驾驶处罚的新规定(一次性扣罚12分)已于2011年4月1日起正式施行.酒后违法驾驶机动车的行为分成两个档次:“酒后驾车”和“醉酒驾车”,其检测标准是驾驶人员血液中的酒精含量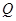 (简称血酒含量,单位是毫克/100毫升),当
(简称血酒含量,单位是毫克/100毫升),当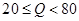 时,为酒后驾车;当
时,为酒后驾车;当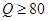 时,为醉酒驾车.某市公安局交通管理部门在某路段的一次拦查行动中,依法检查了200辆机动车驾驶员的血酒含量(如下表).
时,为醉酒驾车.某市公安局交通管理部门在某路段的一次拦查行动中,依法检查了200辆机动车驾驶员的血酒含量(如下表).
依据上述材料回答下列问题:
(Ⅰ)分别写出酒后违法驾车发生的频率和酒后违法驾车中醉酒驾车的频率;
(Ⅱ)从酒后违法驾车的司机中,抽取2人,请一一列举出所有的抽取结果,并求取到的2人中含有醉酒驾车的概率. (酒后驾车的人用大写字母如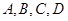 表示,醉酒驾车的人用小写字母如
表示,醉酒驾车的人用小写字母如 表示)
表示)
| 血酒含量 | (0,20) | [20,40) | [40,60) | [60,80) | [80,100) | [100,120] |
| 人数 | 194 | 1 | 2 | 1 | 1 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)一个口袋内装有大小相同的5 个球,其中3个白球分别记为A1、A2、A3;2个黑球分别记为B1、B2,从中一次摸出2个球.
(Ⅰ)写出所有的基本事件;
(Ⅱ)求摸出2球均为白球的概率
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
已知关于x的二次函数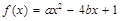 .
.
(I)设集合P={1,2,3}和Q={-1,1,2,3,4},分别从集合P和Q中随机取一个数作为a和b,求函数 在区间
在区间 上是增函数的概率;
上是增函数的概率;
(II)设点(a,b)是区域 内的一点,求函数
内的一点,求函数 在区间
在区间 上是增函数的概率.
上是增函数的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分13分) 已知关于x的二次函数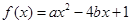
(1)设集合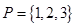 和
和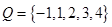 ,从集合
,从集合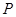 中随机取一个数作为
中随机取一个数作为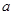 ,从
,从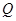 中随机取一个数作为
中随机取一个数作为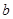 ,求函数
,求函数 在区间
在区间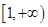 上是增函数的概率;
上是增函数的概率;
(2)设点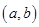 是区域
是区域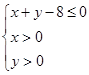 内的随机点,求函数
内的随机点,求函数 在区间
在区间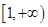 上是增函数的概率.
上是增函数的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)
一个盒子中装有4张卡片,每张卡片上写有1个数字,数字分别是1、2、3、4,现从盒子中随机抽取卡片.
(Ⅰ)若一次从中随机抽取3张卡片,求3张卡片上数字之和大于或等于7的概率;
(Ⅱ)若第一次随机抽取1张卡片,放回后再随机抽取1张卡片,求两次抽取的卡片中至少一次抽到数字2的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知盒中装有仅颜色不同的玻璃球6个,其中红球2个、黑球3个、白球1个.
(1)从中任取1个球, 求取得红球或黑球的概率;
(2)从中一次取2个不同的球,试列出所有基本事件;并求至少有一个是红球概率。
(3)从中取2次,每次取1个球,在放回的条件下求至少有一个是红球概率。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)甲、乙两人各进行一次射击,如果两人击中目标的概率都是0.6,计算:
(1)两人都击中目标的概率;
(2)其中恰有一人击中目标的概率;
(3)至少有一人击中目标的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com