
【题目】2020年1月10日,中国工程院院士黄旭华和中国科学院院士曾庆存荣获2019年度国家最高科学技术奖.曾庆存院士是国际数值天气预报奠基人之一,他的算法是世界数值天气预报核心技术的基础,在气象预报中,过往的统计数据至关重要,如图是根据甲地过去50年的气象记录所绘制的每年高温天数(若某天气温达到35 ℃及以上,则称之为高温天)的频率分布直方图.若某年的高温天达到15天及以上,则称该年为高温年,假设每年是否为高温年相互独立,以这50年中每年高温天数的频率作为今后每年是否为高温年的概率.
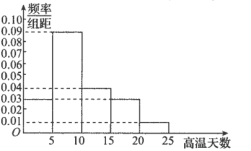
(1)求今后4年中,甲地至少有3年为高温年的概率.
(2)某同学在位于甲地的大学里勤工俭学,成为了校内奶茶店(消费区在户外)的店长,为了减少高温年带来的损失,该同学现在有两种方案选择:方案一:不购买遮阳伞,一旦某年为高温年,则预计当年的收入会减少6000元;方案二:购买一些遮阳伞,费用为5000元,可使用4年,一旦某年为高温年,则预计当年的收入会增加1000元.以4年为期,试分析该同学是否应该购买遮阳伞?
科目:高中数学 来源: 题型:
【题目】某度假酒店为了解会员对酒店的满意度,从中抽取50名会员进行调查,把会员对酒店的“住宿满意度”与“餐饮满意度”都分为五个评分标准:1分(很不满意);2分(不满意);3分(一般);4分(满意);5分(很满意).其统计结果如下表(住宿满意度为![]() ,餐饮满意度为
,餐饮满意度为![]() )
)

(1)求“住宿满意度”分数的平均数;
(2)求“住宿满意度”为3分时的5个“餐饮满意度”人数的方差;
(3)为提高对酒店的满意度,现从![]() 且
且![]() 的会员中随机抽取2人征求意见,求至少有1人的“住宿满意度”为2的概率.
的会员中随机抽取2人征求意见,求至少有1人的“住宿满意度”为2的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】腾飞中学学生积极参加科技创新大赛,在市级组织的大赛中屡创佳绩.为了组织学生参加下一届市级大赛,了解学生报名参加社会科学类比赛(以下称为A类比赛)和自然科学类比赛(以下称为B类比赛)的意向,校团委随机调查了60名男生和40名女生调查结果如下:60名男生中,15名不准备参加比赛,5名准备参加A类比赛和B类比赛,剩余的男生有![]() 准备参加A类比赛,
准备参加A类比赛,![]() 准备参加B类比赛,40名女生中,10名不准备参加比赛,25名准备参加A类比赛,5名准备参加B类比赛.
准备参加B类比赛,40名女生中,10名不准备参加比赛,25名准备参加A类比赛,5名准备参加B类比赛.
(1)根据统计数据,完成如2×2列联表(A类比赛和B类比赛都参加的学生需重复统计):
A类比赛 | B类比赛 | 总计 | |
男生 | |||
女生 | |||
总计 |
(2)能否有99%的把握认为学生参加A类比赛或B类比赛与性别有关?
附:K2![]() .
.
P(K2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我们打印用的A4纸的长与宽的比约为![]() ,之所以是这个比值,是因为把纸张对折,得到的新纸的长与宽之比仍约为
,之所以是这个比值,是因为把纸张对折,得到的新纸的长与宽之比仍约为![]() ,纸张的形状不变.已知圆柱的母线长小于底面圆的直径长(如图所示),它的轴截面ABCD为一张A4纸,若点E为上底面圆上弧AB的中点,则异面直线DE与AB所成的角约为( )
,纸张的形状不变.已知圆柱的母线长小于底面圆的直径长(如图所示),它的轴截面ABCD为一张A4纸,若点E为上底面圆上弧AB的中点,则异面直线DE与AB所成的角约为( )
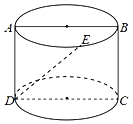
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com