
分析 设f(x)=g(x)+h(x),其中g(x)为奇函数,h(x)为偶函数.f(-x)=g(-x)+h(-x)=-g(x)+h(x),运用函数方程的思想,求得h(x).
解答 解:设f(x)=g(x)+h(x),其中g(x)为奇函数,h(x)为偶函数.
则f(-x)=g(-x)+h(-x)=-g(x)+h(x),
∴h(x)=$\frac{1}{2}$[f(x)+f(-x)]=$\frac{1}{2}$(lg|x+9|-ax+lg|9-x|+ax)=$\frac{1}{2}lg(81-{x}^{2})$.
故答案为:h(x)=$\frac{1}{2}lg(81-{x}^{2})$.
点评 本题考查函数解析式的求解及常用方法,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{3}$ | B. | 6 | C. | ±2$\sqrt{6}$ | D. | ±$\sqrt{15}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2017届湖北襄阳四中高三七月周考三数学(文)试卷(解析版) 题型:选择题
如果命题“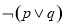 ”为假命题,则( )
”为假命题,则( )
A.p,q均为假命题
B.p,q均为真命题
C.p,q中至少一个为真命题
D.p,q中至多有一个为真命题
查看答案和解析>>
科目:高中数学 来源:2017届河南新乡一中高三9月月考数学(文)试卷(解析版) 题型:选择题
已知三个数 ,
,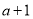 ,
,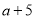 成等比数列,其倒数重新排列后为递增的等比数列
成等比数列,其倒数重新排列后为递增的等比数列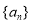 的前三项,则能使不等式
的前三项,则能使不等式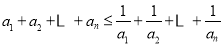 成立的自然数
成立的自然数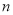 的最大值为( )
的最大值为( )
A.9 B.8 C.7 D.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com