
分析 利用已知条件求出$\overrightarrow{a}$+$\overrightarrow{b}$,m$\overrightarrow{a-}$$\overrightarrow{b}$,通过向量共线求出结果即可.
解答 解:向量$\overrightarrow{a}$=(1,0),$\overrightarrow{b}$=(3,-1),
向量$\overrightarrow{a}$+$\overrightarrow{b}$=(4,-1),
m$\overrightarrow{a-}$$\overrightarrow{b}$=(m-3,1),
向量$\overrightarrow{a}$+$\overrightarrow{b}$与m$\overrightarrow{a-}$$\overrightarrow{b}$共线,
可得3-m=4,
解得m=-1.
故答案为:-1.
点评 本题考查向量共线定理的应用,考查计算能力.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案科目:高中数学 来源:2017届湖北襄阳四中高三七月周考三数学(文)试卷(解析版) 题型:解答题
已知函数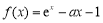 (
(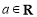 ).
).
(1)求函数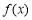 的单调区间;
的单调区间;
(2)函数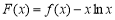 在定义域内存在零点,求
在定义域内存在零点,求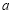 的取值范围.
的取值范围.
(3)若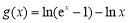 ,当
,当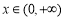 时,不等式
时,不等式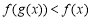 恒成立,求
恒成立,求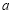 的取值范围
的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2017届湖北襄阳四中高三七月周考三数学(文)试卷(解析版) 题型:选择题
已知定义在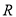 上的奇函数
上的奇函数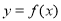 ,对于
,对于 都有
都有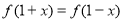 ,当
,当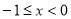 时,
时,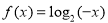 ,则函数
,则函数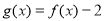 在
在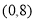 内所有的零点之和为( )
内所有的零点之和为( )
A.6 B.8 C.10 D.12
查看答案和解析>>
科目:高中数学 来源:2017届湖北襄阳四中高三七月周考三数学(理)试卷(解析版) 题型:填空题
函数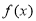 的定义域为
的定义域为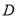 ,若存在闭区间[m,n]
,若存在闭区间[m,n] 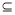 D,使得函数
D,使得函数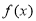 满足:①
满足:①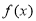 在[m,n]上是单调函数;②
在[m,n]上是单调函数;②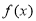 在[m,n]上的值域为[2m,2n],则称区间[m,n]为
在[m,n]上的值域为[2m,2n],则称区间[m,n]为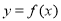 的“倍值区间”.下列函数中存在“倍值区间”的有 .(填上所有正确的序号)
的“倍值区间”.下列函数中存在“倍值区间”的有 .(填上所有正确的序号)
①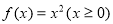 ;
;
② ;
;
③ ;
;
④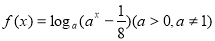 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | 3 | D. | $\frac{9}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com