
| A. | $(0,\frac{{\sqrt{14}}}{3}]$ | B. | $(\frac{{\sqrt{14}}}{3},\sqrt{2}]$ | C. | $(\frac{{\sqrt{5}}}{2},\sqrt{5}]$ | D. | $(\frac{{\sqrt{7}}}{2},\sqrt{7}]$ |
分析 由已知作出图形,设出点O(x,y),|AB1|=a,|AB2|=b,则点P(a,b),结合$|{\overrightarrow{O{B_1}}}|=|{\overrightarrow{O{B_2}}}|=1$求出x2+y2的范围得答案.
解答 解:根据条件知A,B1,P,B2构成一个矩形AB1PB2,
以AB1,AB2所在直线为坐标轴建立直角坐标系,设点O(x,y),|AB1|=a,|AB2|=b,则点P(a,b),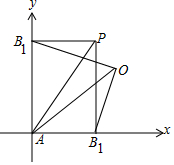
由$|{\overrightarrow{O{B_1}}}|=|{\overrightarrow{O{B_2}}}|=1$,得$\left\{{\begin{array}{l}{{{(x-a)}^2}+{y^2}=1}\\{{x^2}+{{(y-b)}^2}=1}\end{array}}\right.$,则$\left\{{\begin{array}{l}{{{(x-a)}^2}=1-{y^2}}\\{{{(y-b)}^2}=1-{x^2}}\end{array}}\right.$,
∵$\overrightarrow{|{OP}|}<\frac{2}{3}$,∴${(x-a)^2}+{(y-b)^2}<\frac{4}{9}$,
∴$1-{x^2}+1-{y^2}<\frac{4}{9}$,得${x^2}+{y^2}>\frac{14}{9}$,
∵(x-a)2+y2=1,∴y2=1-(x-a)2≤1.
同理x2≤1,∴x2+y2≤2.
综上可知,$\frac{14}{9}<{x^2}+{y^2}≤2$,则$|{\overrightarrow{OA}}|=\sqrt{{x^2}+{y^2}}∈(\frac{{\sqrt{14}}}{3},\sqrt{2}]$.
故选:B.
点评 本题考查平面向量的数量积运算,考查了数形结合的解题思想方法,由题意抽象出图形是关键,是中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | $({\frac{1}{2},1})$ | B. | $({\frac{1}{2},\frac{3}{4}})$ | C. | $({\frac{1}{3},1})$ | D. | $({\frac{1}{2},2})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | S1=1=S2 | B. | S1=1>S2 | C. | S1>1>S2 | D. | S1<1<S2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 15 | B. | 16 | C. | 18 | D. | 31 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com