
分析 利用等比数列的通项公式及其求和公式即可得出.
解答 解:设等比数列{an}的公比为q,∵a3=4,S3=12,
∴${a}_{1}{q}^{2}$=4,${a}_{1}(1+q+{q}^{2})$=12,
解得$\left\{\begin{array}{l}{{a}_{1}=4}\\{q=1}\end{array}\right.$,$\left\{\begin{array}{l}{{a}_{1}=16}\\{q=-\frac{1}{2}}\end{array}\right.$.
∴公比q=1或$-\frac{1}{2}$
故答案为:1或$-\frac{1}{2}$.
点评 本题考查了等比数列的通项公式及其求和公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
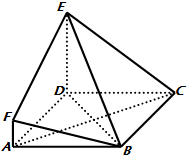 在如图所示的几何体中,四边形ABCD是边长为3的菱形,∠DAB=60°,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°.
在如图所示的几何体中,四边形ABCD是边长为3的菱形,∠DAB=60°,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3米/秒 | B. | 4米/秒 | C. | 5米/秒 | D. | 2米/秒 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 使用年限x | 1 | 2 | 3 | 4 |
| 总费用y | 1.5 | 2 | 3 | 3.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一或第三象限角 | B. | 第二或第三象限角 | ||
| C. | 第一或第四象限角 | D. | 第二或第四象限角 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{2\sqrt{2}+\sqrt{3}}}{6}$ | B. | $\frac{{2\sqrt{2}-\sqrt{3}}}{6}$ | C. | $\frac{{\sqrt{2}+2\sqrt{3}}}{6}$ | D. | $\frac{{\sqrt{2}-2\sqrt{3}}}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
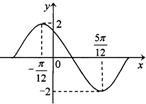 函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)在一个周期内的图象如图.
函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)在一个周期内的图象如图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com