
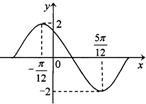
 函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)在一个周期内的图象如图.
函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)在一个周期内的图象如图.分析 (1)由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,可得函数的解析式.
(2)利用正弦函数的单调性,求得函数f(x)的单调增区间.
(3)根据f(x)得解析式,利用正弦函数的定义域和值域,求得函数f(x)的值域.
解答 解:(1)根据函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)在一个周期内的图象,
可得A=2,$\frac{1}{2}•\frac{2π}{ω}$=$\frac{5π}{12}$-(-$\frac{π}{12}$),∴ω=2.
再根据五点法作图可得2•(-$\frac{π}{12}$)+φ=$\frac{π}{2}$,∴φ=$\frac{2π}{3}$,∴f(x)=2sin(2x+$\frac{2π}{3}$).
(2)令2kπ-$\frac{π}{2}$≤2x+$\frac{2π}{3}$≤2kπ+$\frac{π}{2}$,求得 kπ-$\frac{7π}{12}$≤x≤kπ-$\frac{π}{12}$,故函数的增区间为[kπ-$\frac{7π}{12}$,kπ-$\frac{π}{12}$],k∈Z.
(3)由f(x)=2sin(2x+$\frac{2π}{3}$),利用正弦函数的值域,可得它的值域为[-2,2].
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值.正弦函数的单调性、定义域和值域,属于中档题.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,一个大风车的半径是8米,每12分钟旋转一周,最低点离地面2米,若风车翼片从最低点按逆时针方向开始旋转,则该翼片的端点P离地面的距离h(米)与时间t(分钟)之间的函数关系是( )
如图,一个大风车的半径是8米,每12分钟旋转一周,最低点离地面2米,若风车翼片从最低点按逆时针方向开始旋转,则该翼片的端点P离地面的距离h(米)与时间t(分钟)之间的函数关系是( )| A. | h=-8sin($\frac{π}{6}$t)+10 | B. | h=-8cos($\frac{π}{3}$t)+10 | C. | h=8cos($\frac{π}{6}$t)+10 | D. | h=-8cos($\frac{π}{6}$t)+10 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
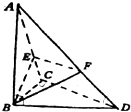 如图,在三棱锥A-BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E,F分别是AC,AD上的动点.且$\frac{AE}{AC}$=$\frac{AF}{AD}$=λ(0<λ<1).
如图,在三棱锥A-BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E,F分别是AC,AD上的动点.且$\frac{AE}{AC}$=$\frac{AF}{AD}$=λ(0<λ<1).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com