
【题目】甘肃省是土地荒漠化较为严重的省份,一代代治沙人为了固沙、治沙,改善生态环境,不断地进行研究与实践,实现了沙退人进.2019年,古浪县八步沙林场“六老汉”三代人治沙群体作为优秀代表,被中宣部授予“时代楷模”称号.在治沙过程中为检测某种固沙方法的效果,治沙人在某一实验沙丘的坡顶和坡腰各布设了50个风蚀插钎,以测量风蚀值(风蚀值是测量固沙效果的指标之一,数值越小表示该插钎处被风吹走的沙层厚度越小,说明固沙效果越好,数值为0表示该插针处没有被风蚀)通过一段时间的观测,治沙人记录了坡顶和坡腰全部插钎测得的风蚀值(所测数据均不为整数),并绘制了相应的频率分布直方图.

(Ⅰ)根据直方图估计“坡腰处一个插钎风蚀值小于30”的概率;
(Ⅱ)若一个插钎的风蚀值小于30,则该数据要标记“*”,否则不标记.根据以上直方图,完成列联表:
标记 | 不标记 | 合计 | |
坡腰 | |||
坡顶 | |||
合计 |
并判断是否有![]() 的把握认为数据标记“*”与沙丘上插钎所布设的位置有关?
的把握认为数据标记“*”与沙丘上插钎所布设的位置有关?
(Ⅲ)坡顶和坡腰的平均风蚀值分别为![]() 和
和![]() ,若
,若![]() ,则可认为此固沙方法在坡顶和坡腰的固沙效果存在差异,试根据直方图计算
,则可认为此固沙方法在坡顶和坡腰的固沙效果存在差异,试根据直方图计算![]() 和
和![]() (同一组中的数据用该组区间的中点值为代表),并判断该固沙方法在坡顶和坡腰的固沙效果是否存在差异.
(同一组中的数据用该组区间的中点值为代表),并判断该固沙方法在坡顶和坡腰的固沙效果是否存在差异.
附:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源: 题型:
【题目】“珠算之父”程大位是我国明代著名的数学家,他的应用巨著《算法统综》中有一首“竹筒容米”问题:“家有九节竹一茎,为因盛米不均平,下头三节四升五,上梢四节三升八,唯有中间两节竹,要将米数次第盛,若有先生能算法,也教算得到天明.”((注)四升五:4.5升,次第盛:盛米容积依次相差同一数量.)用你所学的数学知识求得中间两节竹的容积为
A. 2.2升B. 2.3升
C. 2.4升D. 2.5升
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在贯彻中共中央国务院关于精准扶贫政策的过程中,某单位定点帮扶100户贫困户.工作组对这100户村民的贫困状况和家庭成员受教育情况进行了调查:甲村55户贫困村民中,家庭成员接受过中等及以上教育的只有10户,乙村45户贫困村民中,家庭成员接受过中等及以上教育的有20户.
(1)完成下面的列联表,并判断是否有99.5%的把握认为贫困与接受教育情况有关;
家庭成员接受过中等以下 教育的户数 | 家庭成员接受过中等及以上 教育的户数 | 合计 | |
甲村贫困户数 | |||
乙村贫困户数 | |||
合计 |
(2)在被帮扶的100户贫困户中,按分层抽样的方法从家庭成员接受过中等及以上教育的贫困户中抽取6户,再从这6户中采用简单随机抽样的方法随机抽取2户,求这2户中甲、乙两村恰好各1户的概率.
参考公式与数据: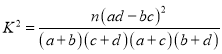 ,其中
,其中![]() .
.
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 是由正整数组成的无穷数列.若存在常数
是由正整数组成的无穷数列.若存在常数![]() ,使得
,使得![]() 任意的
任意的![]() 成立,则称数列
成立,则称数列![]() 具有性质
具有性质![]() .
.
(1)分别判断下列数列![]() 是否具有性质
是否具有性质![]() ; (直接写出结论)
; (直接写出结论)
①![]()
②![]()
(2)若数列![]() 满足
满足![]() ,求证:“数列
,求证:“数列![]() 具有性质
具有性质![]() ”是“数列
”是“数列![]() 为常数列”的充分必要条件;
为常数列”的充分必要条件;
(3)已知数列![]() 中
中![]() 且
且![]() .若数列
.若数列![]() 具有性质
具有性质![]() ,求数列
,求数列![]() 的通项公式.
的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近五年来某草场羊只数量与草场植被指数两变量间的关系如表所示,绘制相应的散点图,如图所示:
年份 | 1 | 2 | 3 | 4 | 5 |
羊只数量(万只) | 1.4 | 0.9 | 0.75 | 0.6 | 0.3 |
草地植被指数 | 1.1 | 4.3 | 15.6 | 31.3 | 49.7 |

根据表及图得到以下判断:①羊只数量与草场植被指数成减函数关系;②若利用这五组数据得到的两变量间的相关系数为![]() ,去掉第一年数据后得到的相关系数为
,去掉第一年数据后得到的相关系数为![]() ,则
,则![]() ;③可以利用回归直线方程,准确地得到当羊只数量为2万只时的草场植被指数;以上判断中正确的个数是( )
;③可以利用回归直线方程,准确地得到当羊只数量为2万只时的草场植被指数;以上判断中正确的个数是( )
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近五年来某草场羊只数量与草场植被指数两变量间的关系如表所示,绘制相应的散点图,如图所示:
年份 | 1 | 2 | 3 | 4 | 5 |
羊只数量(万只) | 1.4 | 0.9 | 0.75 | 0.6 | 0.3 |
草地植被指数 | 1.1 | 4.3 | 15.6 | 31.3 | 49.7 |

根据表及图得到以下判断:①羊只数量与草场植被指数成减函数关系;②若利用这五组数据得到的两变量间的相关系数为![]() ,去掉第一年数据后得到的相关系数为
,去掉第一年数据后得到的相关系数为![]() ,则
,则![]() ;③可以利用回归直线方程,准确地得到当羊只数量为2万只时的草场植被指数;以上判断中正确的个数是( )
;③可以利用回归直线方程,准确地得到当羊只数量为2万只时的草场植被指数;以上判断中正确的个数是( )
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣1|+|2x+2|,g(x)=|x+2|﹣|x﹣2a|+a.
(1)求不等式f(x)>4的解集;
(2)对x1∈R,x2∈R,使得f(x1)≥g(x2)成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年春节期间,新型冠状病毒(2019﹣nCoV)疫情牵动每一个中国人的心,危难时刻全国人民众志成城.共克时艰,为疫区助力.我国S省Q市共100家商家及个人为缓解湖北省抗疫消毒物资压力,募捐价值百万的物资对口输送湖北省H市.
(1)现对100家商家抽取5家,其中2家来自A地,3家来自B地,从选中的这5家中,选出3家进行调研.求选出3家中1家来自A地,2家来自B地的概率.
(2)该市一商家考虑增加先进生产技术投入,该商家欲预测先进生产技术投入为49千元的月产增量.现用以往的先进技术投入xi(千元)与月产增量yi(千件)(i=1,2,3,…,8)的数据绘制散点图,由散点图的样本点分布,可以认为样本点集中在曲线![]() 的附近,且:
的附近,且:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其中,
,其中,![]() ,
,![]() ,根据所给的统计量,求y关于x回归方程,并预测先进生产技术投入为49千元时的月产增量.
,根据所给的统计量,求y关于x回归方程,并预测先进生产技术投入为49千元时的月产增量.
附:对于一组数据(u1,v1)(u2,v2),其回归直线v=α+βu的斜率和截距的最小二乘法估计分别为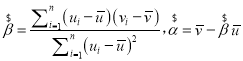
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com