
分析 利用导函数研究函数f(x)的单调性,利用单调性求其值域.
解答 解:函数f(x)=$\frac{xln(x-1)}{x-2}$,x∈[1.5,3],且x≠2.
则f′(x)=$\frac{[xln(x-1)]′(x-2)-(x-2)′[xln(x-1)]}{(x-2)^{2}}$,
令f′(x)=0,
解得:x=2.
∵x∈[1.5,3],且x≠2.
当1.5≤x<2,f′(x)<0,故而f(x)是单调递减,且f(x)>0.
当2<x≤3,f′(x)>0,故而f(x)是单调递增,且f(x)>0.
∴f(x)>0.
当x=3时,取得最大值为3ln2.
得函数f(x)的值域为(0,3ln2].
故答案为:(0,3ln2].
点评 本题考查了函数值域的求法.高中函数值域求法有:1、观察法,2、配方法,3、反函数法,4、判别式法;5、换元法,6、数形结合法,7、不等式法,8、分离常数法,9、单调性法,10、利用导数求函数的值域,11、最值法,12、构造法,13、比例法.要根据题意选择.


科目:高中数学 来源: 题型:选择题
| A. | ①④ | B. | ②④ | C. | ②③ | D. | ②③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 50 | B. | 51 | C. | 100 | D. | 101 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2k+$\frac{3}{4}$<a<2k+$\frac{5}{4}$,k∈Z | B. | 2k+1<a<2k+3,k∈Z | ||
| C. | 2k+1<a<2k+$\frac{5}{4}$,k∈Z | D. | 2k-$\frac{3}{4}$<a<2k+1,k∈Z |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
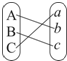 连线方式表示为$(\begin{array}{l}{A^{\;}}{B^{\;}}C\\{b^{\;}}{c^{\;}}a\end{array})$,规定第一行A,B,C的顺序固定不变,请列出所有连线的情况;
连线方式表示为$(\begin{array}{l}{A^{\;}}{B^{\;}}C\\{b^{\;}}{c^{\;}}a\end{array})$,规定第一行A,B,C的顺序固定不变,请列出所有连线的情况;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com