
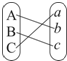
 连线方式表示为$(\begin{array}{l}{A^{\;}}{B^{\;}}C\\{b^{\;}}{c^{\;}}a\end{array})$,规定第一行A,B,C的顺序固定不变,请列出所有连线的情况;
连线方式表示为$(\begin{array}{l}{A^{\;}}{B^{\;}}C\\{b^{\;}}{c^{\;}}a\end{array})$,规定第一行A,B,C的顺序固定不变,请列出所有连线的情况;分析 (Ⅰ)结合题意作出所有连线的情况即可;
(II)参赛者得0分,说明该参赛者恰连对一条,从而求概率.
解答 解:(I)所有连线情况如下$(\begin{array}{l}{A^{\;}}{B^{\;}}C\\{a^{\;}}{b^{\;}}c\end{array})$$(\begin{array}{l}{A^{\;}}{B^{\;}}C\\{a^{\;}}{c^{\;}}b\end{array})$$(\begin{array}{l}{A^{\;}}{B^{\;}}C\\{c^{\;}}{b^{\;}}a\end{array})$$(\begin{array}{l}{A^{\;}}{B^{\;}}C\\{b^{\;}}{a^{\;}}c\end{array})$$(\begin{array}{l}{A^{\;}}{B^{\;}}C\\{b^{\;}}{c^{\;}}a\end{array})$$(\begin{array}{l}{A^{\;}}{B^{\;}}C\\{c^{\;}}{a^{\;}}b\end{array})$…(6分)
注:每列对一个给(1分)
(II)参赛者得0分,说明该参赛者恰连对一条
所以该参赛者得0分的概率为$P=\frac{3}{6}=\frac{1}{2}$…(12分)
点评 解决的关键是对于古典概型概率的运用,属于基础题.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{5π}{6}$ | B. | $\frac{3π}{4}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{9}$ | B. | $\frac{5}{9}$ | C. | $\frac{8}{27}$ | D. | $\frac{19}{27}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
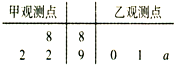 如图,茎叶图记录了某城市甲、乙两个观测点连续三天观测到的空气质量指数(AQI).乙观测点记录中有一个数字模糊无法确认,已知该数是0,1,…,9中随机的一个数,并在图中以a表示.
如图,茎叶图记录了某城市甲、乙两个观测点连续三天观测到的空气质量指数(AQI).乙观测点记录中有一个数字模糊无法确认,已知该数是0,1,…,9中随机的一个数,并在图中以a表示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在四棱锥P-ABCD中,PA⊥底面ABCD,AB∥CD,AB⊥BC,PA=AB=BC=$\frac{1}{2}$CD.
在四棱锥P-ABCD中,PA⊥底面ABCD,AB∥CD,AB⊥BC,PA=AB=BC=$\frac{1}{2}$CD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a3<b3 | B. | ab>b2 | C. | ac2>bc2 | D. | $\frac{1}{a}$<$\frac{1}{b}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
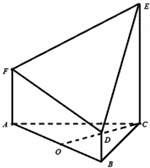 如图所示的几何体是由等边三角形ABC的底面的棱柱被平面DEF所截得,已知FA⊥平面ABC,AB=2,BD=1,AF=2,CE=3,O为AB的中点.
如图所示的几何体是由等边三角形ABC的底面的棱柱被平面DEF所截得,已知FA⊥平面ABC,AB=2,BD=1,AF=2,CE=3,O为AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com