
【题目】已知椭圆:![]() (a>b>0)过点E(
(a>b>0)过点E(![]() ,1),其左、右顶点分别为A,B,左、右焦点为F1,F2,其中F1(
,1),其左、右顶点分别为A,B,左、右焦点为F1,F2,其中F1(![]() ,0).
,0).
(1)求椭圆C的方程:
(2)设M(x0,y0)为椭圆C上异于A,B两点的任意一点,MN⊥AB于点N,直线l:x0x+2y0y﹣4=0,设过点A与x轴垂直的直线与直线l交于点P,证明:直线BP经过线段MN的中点.
【答案】(1)![]() ;(2)证明详见解析.
;(2)证明详见解析.
【解析】
(1)根据椭圆上一点到两焦点的距离之和为2a,可求出a,已知焦点坐标,可知c,可求方程.
(2)根据题意求出ABP的坐标,求PB直线方程,求出点N坐标,求出其中点,可代入判断在直线PB上.
(1)由题意知,2a=|EF1|+|EF2|![]() 4,
4,
则a=2,c![]() ,b
,b![]() ,
,
故椭圆的方程为![]() ,
,
(2)由(1)知A(﹣2,0),B(2,0),
过点A且与x轴垂直的直线的方程为x=﹣2,
结合方程x0x+2y0y﹣4=0,得点P(﹣2,![]() ),
),
直线PB的斜率为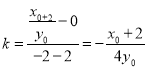 ,
,
直线PB的方程为![]() ,
,
因为MN⊥AB于点N,所以N(x0,0),线段MN的中点坐标(![]() ),
),
令x=x0,得![]() ,
,
因为![]() ,所以
,所以![]() ,
,
即直线BP经过线段MN的中点.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:高中数学 来源: 题型:
【题目】某中学为研究学生的身体素质与体育锻炼时间的关系,对该校200名高三学生平均每天体育锻炼时间进行调查,如表:(平均每天锻炼的时间单位:分钟)
平均每天锻炼的时间/分钟 |
|
|
|
|
|
|
总人数 | 20 | 36 | 44 | 50 | 40 | 10 |
将学生日均体育锻炼时间在![]() 的学生评价为“锻炼达标”.
的学生评价为“锻炼达标”.
(1)请根据上述表格中的统计数据填写下面![]() 列联表;
列联表;
锻炼不达标 | 锻炼达标 | 合计 | |
男 | |||
女 | 20 | 110 | |
合计 |
并通过计算判断,是否能在犯错误的概率不超过0.025的前提下认为“锻炼达标”与性别有关?
(2)在“锻炼达标”的学生中,按男女用分层抽样方法抽出5人,进行体育锻炼体会交流,从参加体会交流的5人中,随机选出2人作重点发言,求恰好选出一名男生的概率.
参考公式: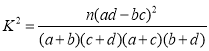 ,其中
,其中![]()
临界值表
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥![]() 中,
中,![]() ,
,![]() 分别是线段
分别是线段![]() ,
,![]() 的中点,底面
的中点,底面![]() 是正三角形,延长
是正三角形,延长![]() 到点
到点![]() ,使得
,使得![]() .
.
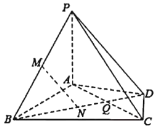
(1)![]() 为线段
为线段![]() 上确定一点,当
上确定一点,当![]() 平面
平面![]() 时,求
时,求![]() 的值;
的值;
(2)当![]() 平面
平面![]() ,且
,且![]() 时,求二面角
时,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点F为椭圆![]() (a>b>0)的一个焦点,点A为椭圆的右顶点,点B为椭圆的下顶点,椭圆上任意一点到点F距离的最大值为3,最小值为1.
(a>b>0)的一个焦点,点A为椭圆的右顶点,点B为椭圆的下顶点,椭圆上任意一点到点F距离的最大值为3,最小值为1.
(1)求椭圆的标准方程;
(2)若M、N在椭圆上但不在坐标轴上,且直线AM∥直线BN,直线AN、BM的斜率分别为k1和k2,求证:k1k2=e2﹣1(e为椭圆的离心率).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国著名数学家华罗庚先生曾说:数缺形时少直观,形缺数时难入微,数形结合百般好,隔裂分家万事休.在数学的学习和研究中,常用函数的图象研究函数的性质,也常用函数的解析式来琢磨函数的图象特征.如函数![]() 的图象大致为( )
的图象大致为( )
A. B.
B.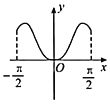
C.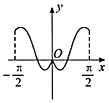 D.
D.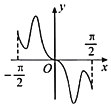
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C1的参数方程为![]() (θ为参数),以原点为极点,x轴非负半轴为极轴,建立极坐标系,曲线C2的极坐标方程为
(θ为参数),以原点为极点,x轴非负半轴为极轴,建立极坐标系,曲线C2的极坐标方程为![]() .
.
(1)求曲线C1的极坐标方程以及曲线C2的直角坐标方程;
(2)若直线l:y=kx与曲线C1、曲线C2在第一象限交于P、Q,且|OQ|=|PQ|,点M的直角坐标为(1,0),求△PMQ的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,椭圆
中,椭圆![]() :
:![]() 过点
过点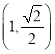 ,且椭圆的离心率为
,且椭圆的离心率为![]() ,直线
,直线![]() :
:![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 、
、![]() 两点,线段
两点,线段![]() 的中垂线交椭圆
的中垂线交椭圆![]() 于
于![]() 、
、![]() 两点.
两点.
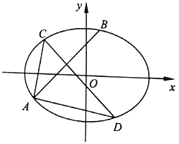
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)求线段![]() 长的最大值;
长的最大值;
(3)求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com