
分析 先根据正△ABC中,$\overrightarrow{AB}$在$\overrightarrow{BC}$方向上的投影为-1,得到正△ABC的边长为2,再根据向量的加减的几何意义和向量的数量积的运算求出答案即可.
解答 解:∵正△ABC中,$\overrightarrow{AB}$在$\overrightarrow{BC}$方向上的投影为-1,
∴正△ABC的边长为2,
∴$\overrightarrow{BD}•\overrightarrow{AC}$=($\overrightarrow{AD}$-$\overrightarrow{AB}$)•$\overrightarrow{AC}$=($\frac{2}{3}$$\overrightarrow{AC}$-$\overrightarrow{AB}$)$•\overrightarrow{AC}$=$\frac{2}{3}$${\overrightarrow{AC}}^{2}$-$\overrightarrow{AB}•\overrightarrow{AC}$=$\frac{2}{3}×{2}^{2}$-2×2×$\frac{1}{2}$=$\frac{2}{3}$,
故答案为:$\frac{2}{3}$.
点评 本题考查了向量加减的几何意义,向量数量积的计算,直接利用定义不易求解,这里利用平面向量基本定理,进行转化计算.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | {-1,0} | B. | {0,1} | C. | {-1,0,1} | D. | {-1,0,1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图是一次摄影大赛上7位评委给某参赛作品打出的分数的茎叶图.记分员在去掉一个最高分和一个最低分后,算得平均分为91分,复核员在复核时,发现有一个数字(茎叶图中的x)无法看清,若记分员计算无误,则数字x应该是1.
如图是一次摄影大赛上7位评委给某参赛作品打出的分数的茎叶图.记分员在去掉一个最高分和一个最低分后,算得平均分为91分,复核员在复核时,发现有一个数字(茎叶图中的x)无法看清,若记分员计算无误,则数字x应该是1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
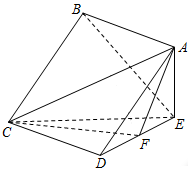 如图,在四棱锥E-ABCD中,底面ABCD是边长为$\sqrt{2}$的正方形,平面AEC⊥平面CDE,∠AEC=90°,F为DE中点,且DE=1.
如图,在四棱锥E-ABCD中,底面ABCD是边长为$\sqrt{2}$的正方形,平面AEC⊥平面CDE,∠AEC=90°,F为DE中点,且DE=1.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -4 | B. | $\frac{1}{4}$ | C. | 4 | D. | -$\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com