
分析 先利用组合求出10个点中取4个点的所有的基本事件个数;利用分类讨论的方法求出取出的四点在一个平面上的所有的基本事件个数;利用对立事件求出不共面的所有的基本的事件个数;利用古典概型概率公式求出这四个点不共面的概率.
解答 解:10个点中取4个点的取法为C104=210种
只要求出共面的就可以了
共面的分三种情况:
①、四个点都在四面体的某一个面上,每个面6个点,有 C64=15种,四个面共有4*15=60种情况.
②、其中三点共线,另一个点与此三点不在四面体的某一个面上,
而在与此三点所在直线异面的那条直线的中点,
显然只有6种情况(因为四面体只有6条边).
③、其中两点所在直线与另两点所在直线平行,
且这四个点也不在四面体的某一个面上,画图可得出只有3种情况.
因此,取四个不共面的点的不同取法共有:210-60-6-3=141
所以这四个点不共面的概率为$\frac{141}{210}$=$\frac{47}{70}$.
故答案为:$\frac{47}{70}$.
点评 本题考查利用排列、组合求完成事件的方法数、考查分类讨论的数学思想方法、考查对立事件的概率的求法.


科目:高中数学 来源: 题型:选择题
| A. | k | B. | -k | C. | $\frac{1}{k}$ | D. | -$\frac{1}{k}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\sqrt{3}+2$ | B. | 1 | C. | 3 | D. | $\frac{\sqrt{3}}{2}+2$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
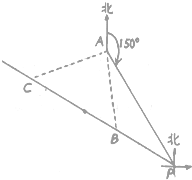 海滨某城市A附近海面上有一台风,在城市A测得该台风中心位于方位角150°、距离400km的海面P处,并正以70km/h的速度沿北偏西60°的方向移动,如果台风侵袭的范围是半径为250km的圆形区域.
海滨某城市A附近海面上有一台风,在城市A测得该台风中心位于方位角150°、距离400km的海面P处,并正以70km/h的速度沿北偏西60°的方向移动,如果台风侵袭的范围是半径为250km的圆形区域.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com