
分析 (1)求出f(x)的导数,讨论m=4,m>4,由导数大于0,可得增区间;
(2)假设存在m<0,使得命题成立.求出f(x)的导数,及单调区间,可得f(x)最大值,g(x)的最小值,即[f(x1)-g(x2)]max≤1,亦即f(x1)max-g(x2)min≤1恒成立.得到m的不等式,即可得到m的范围;
(3)设函数h(x)=x2+mx+n的两个零点为x1、x2(0<x1,x2<1),则f(x)=(x-x1)(x-x2),n(1+m+n)=f(0)f(1),运用基本不等式即可得到所求范围.
解答 解:(1)f'(x)=mx2-(4+m)x+4=(x-1)(mx-4)---------(2分)
当m=4时,f'(x)=4(x-1)2≥0,∴f(x)在(-∞,+∞)上单增,---------(3分)
当m>4时,$\frac{4}{m}<1$,∴f(x)的递增区间为$(-∞,\frac{4}{m}),\;(1,+∞)$.---------(4分)
(2)假设存在m<0,使得命题成立,此时$f'(x)=m(x-1)(x-\frac{4}{m})$.
∵m<0,∴$\frac{4}{m}<1$.
则f(x)在$(-∞,\frac{4}{m})$和(1,+∞)递减,在$(\frac{4}{m},1)$递增.
∴f(x)在[2,3]上递减,又g(x)在[2,3]递增.
∴$f{(x)_{max}}=f(2)=\frac{2}{3}m+1,\;g{(x)_{min}}=g(2)=2+m$.---------(6分)
因此,对x1,x2∈[2,3],f(x1)-g(x2)≤1恒成立.
即[f(x1)-g(x2)]max≤1,亦即f(x1)max-g(x2)min≤1恒成立.
∴$\frac{2}{3}m+1-(2+m)≤1$∴m≥-6.又m<0故m的范围为[-6,0).-------(8分)
(3)设函数h(x)=x2+mx+n的两个零点为x1、x2(0<x1,x2<1),
则f(x)=(x-x1)(x-x2).
又f(0)=n=x1x2>0,f(1)=1+m+n=(1-x1)(1-x2)>0,-------(10分)
∴n(1+m+n)=f(0)f(1).
而$0<f(0)f(1)={x_1}{x_2}(1-{x_1})(1-{x_2})≤{(\frac{{{x_1}+1-{x_1}}}{2})^2}{(\frac{{{x_2}+1-{x_2}}}{2})^2}=\frac{1}{16}$,
由于x1≠x2,故$0<f(0)f(1)<\frac{1}{16}$,∴$0<n(1+m+n)<\frac{1}{16}$.…(12分)
点评 本题考查导数的运用:求单调区间和极值、最值,考查不等式恒成立问题合函数零点问题的解法,注意运用转化思想和分类法,以及基本不等式,考查化简整理的运算能力,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{5}{4}$ | C. | 1 | D. | 2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
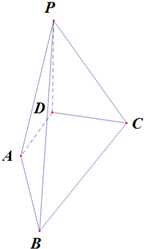 如图,PD⊥平面ABCD,AD⊥DC,AD∥BC,PD:DC:BC=1:1:$\sqrt{2}$.
如图,PD⊥平面ABCD,AD⊥DC,AD∥BC,PD:DC:BC=1:1:$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | 0 | D. | $-\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(1)<f(-1)<c | B. | f(-1)<c<f(1) | C. | f(1)<c<f(3) | D. | c<f(3)<f(1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com