
分析 (Ⅰ)求出f(x)的导数,求出切线斜率和切点,由点斜式方程可得切线方程;
(Ⅱ)当x>1时,f(x)+$\frac{a}{x}$<0恒成立,等价于k<$\frac{1}{2}$x2-xlnx,构造函数,求最值,即可求实数k的取值范围;
(Ⅲ)证明$\frac{1}{xlnx}$>$\frac{2}{{x}^{2}-1}$=$\frac{1}{x-1}$-$\frac{1}{x+1}$,把x=1,2,…n分别代入上面不等式,并相加得结论.
解答 解:(Ⅰ)∵f(x)=lnx-$\frac{1}{2}$x,
∴f′(x)=$\frac{1}{x}$-$\frac{1}{2}$,
f(x)的图象在点(1,f(1))处的切线斜率为$\frac{1}{2}$,
切点为(1,-$\frac{1}{2}$),
f(x)的图象在点(1,f(1))处的切线方程为y+$\frac{1}{2}$=$\frac{1}{2}$(x-1),
即为x-2y-2=0;
(Ⅱ)当x>1时,f(x)+$\frac{a}{x}$<0恒成立,等价于k<$\frac{1}{2}$x2-xlnx,
令g(x)=$\frac{1}{2}$x2-xlnx,则g′(x)=x-1-lnx.
令h(x)=x-1-lnx,则h′(x)=$\frac{x-1}{x}$.
当x>1时,h′(x)>0,函数h(x)在(1,+∞)上单调递增,
故h(x)>h(1)=0,
从而,当x>1时,g′(x)>0,即函数g(x)在(1,+∞)上单调递增,
故g(x)>g(1)=$\frac{1}{2}$.
∴k≤$\frac{1}{2}$;
(Ⅲ)证明:由(Ⅱ)得,当x>1时,lnx-$\frac{1}{2}$x+$\frac{1}{2x}$<0,
可化为xlnx<$\frac{{x}^{2}-1}{2}$,
又xlnx>0,
从而,$\frac{1}{xlnx}$>$\frac{2}{{x}^{2}-1}$=$\frac{1}{x-1}$-$\frac{1}{x+1}$.
把x=2,…n分别代入上面不等式,并相加得,
$\frac{1}{2ln2}$+$\frac{1}{3ln3}$+…+$\frac{1}{nlnn}$>1-$\frac{1}{3}$+$\frac{1}{2}$-$\frac{1}{4}$+…+$\frac{1}{n-1}$-$\frac{1}{n+1}$=1+$\frac{1}{2}$-$\frac{1}{n}$-$\frac{1}{n+1}$=$\frac{3{n}^{2}-n-2}{2{n}^{2}+2n}$.
点评 本题属导数的综合应用题,考查学生会利用导数求曲线上过某点切线方程,会利用导数研究函数的最值,考查不等式的证明,有难度.


 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
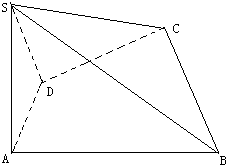 如图四棱锥S-ABCD,底面四边形ABCD满足条件∠DAB=90°,∠ADC=135°,AB=5,CD=2$\sqrt{2}$,AD=2,侧面SAD垂直于底面ABCD,SA=2,
如图四棱锥S-ABCD,底面四边形ABCD满足条件∠DAB=90°,∠ADC=135°,AB=5,CD=2$\sqrt{2}$,AD=2,侧面SAD垂直于底面ABCD,SA=2,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
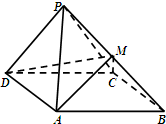 如图,四棱锥P-ABCD中,侧面PDC是边长为2的正三角形,底面ABCD是菱形,∠ADC=60°,点P在底面ABCD上的射影为△ACD的重心,点M为线段PB上的点.
如图,四棱锥P-ABCD中,侧面PDC是边长为2的正三角形,底面ABCD是菱形,∠ADC=60°,点P在底面ABCD上的射影为△ACD的重心,点M为线段PB上的点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com