
分析 (1)由于2011=91×22+9,可得q,r.
(2)集合B={5,7,8,9,11,12,t}满足B⊆A,但B不为“和谐集”,经过验证可得:所有满足条件的t值为:13,17,19,23.
(3)当m=8时,记M={7+i|i=1,2,…,16},N={2(7+i)|i=1,2,3,4},记P=CMN,则card(P)=12,显然对任意1≤i<j≤16,不存在n≥3,使得7+j=n(7+i)成立.故P是非“和谐集”,此时P={8,9,10,11,12,13,14,15,17,19,21,23}.同样的,当m=9,10,11,12时,存在含m的集合A的有12个元素的子集为非“和谐集”.因此m≤7.下面再证明:含7的任意集合A的有12个元素的子集为“和谐集”即可.
解答 解:(1)∵2011=91×22+9,∴q=22,r=9.
(2)集合B={5,7,8,9,11,12,t}满足B⊆A,但B不为“和谐集”,经过验证可得:
所有满足条件的t值为:13,17,19,23.
(3)当m=8时,记M={7+i|i=1,2,…,16},N={2(7+i)|i=1,2,3,4}记P=CMN,则card(P)=12,显然对任意1≤i<j≤16,不存在n≥3,使得7+j=n(7+i)成立.故P是非“和谐集”,此时P={8,9,10,11,12,13,14,15,17,19,21,23}.同样的,当m=9,10,11,12时,存在含m的集合A的有12个元素的子集为非“和谐集”.因此m≤7.
下面证明:含7的任意集合A的有12个元素的子集为“和谐集”.
设B={a1,a2,…,a11,7},若1,14,21中之一为集合B的元素,显然为“和谐集”.
现考虑1,14,21都不属于集合B,构造集合B1={2,4,8,16},B2={3,6,12},B3={5,10,20},B4={9,18},B5={11,22},B'={13,15,17,19,23}.
以上B1,B2,B3,B4,B5每个集合中的元素都是倍数关系.考虑B'⊆B的情况,也即B'中5个元素全都是B的元素,B中剩下6个元素必须从B1,B2,B3,B4,B5这5个集合中选取6个元素,那么至少有一个集合有两个元素被选,即集合B中至少有两个元素存在倍数关系.
综上所述,含7的任意集合A的有12个元素的子集B为“和谐集”,即m的最大值为7.
点评 本题考查了新定义“和谐集”、分类讨论思想方法、数的整除理论,考查了推理能力与计算能力,属于难题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
 已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分别是线段AB、BC的中点.
已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分别是线段AB、BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
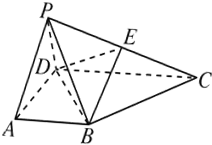 已知在四棱锥P-ABCD中,底面ABCD是直角梯形,∠BAD=90°,2AB=2AD=CD,侧面PAD是正三角形且垂直于底面ABCD,E是PC的中点.
已知在四棱锥P-ABCD中,底面ABCD是直角梯形,∠BAD=90°,2AB=2AD=CD,侧面PAD是正三角形且垂直于底面ABCD,E是PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
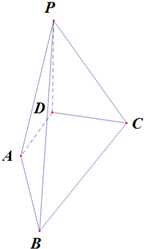 如图,PD⊥平面ABCD,AD⊥DC,AD∥BC,PD:DC:BC=1:1:$\sqrt{2}$.
如图,PD⊥平面ABCD,AD⊥DC,AD∥BC,PD:DC:BC=1:1:$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | 0 | D. | $-\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com