
分析 (Ⅰ)去掉绝对值,讨论函数f(x)的单调性,从而得出f(x)在[-$\frac{1}{2}$,$\frac{1}{2}$]上的单调性.
(Ⅱ)求出使不等式f(x)>2|x-a|对任意x∈R时都成立的a的取值范围,再求使不等式f(x)≤2|x-a|有解的a的取值范围.
解答 解:(Ⅰ)若a=1,函数f(x)=x2+|x|=$\left\{\begin{array}{l}{{x}^{2}-x,-\frac{1}{2}≤x<0}\\{{x}^{2}+x,0≤x≤\frac{1}{2}}\end{array}\right.$,
故f(x)在[-$\frac{1}{2}$,0)上是减函数,在[0,$\frac{1}{2}$]上是增函数.
(Ⅱ)先求使不等式f(x)>2|x-a|对x∈R恒成立时a的取值范围.
①当x≤a-1时,不等式化为x2-x-1+a>2(a-x),即x2+x-1>a,∴${(x+\frac{1}{2})}^{2}$-$\frac{5}{4}$>a,
若a-1≥-$\frac{1}{2}$,即a≥$\frac{1}{2}$,则由不等式可得a<-$\frac{5}{4}$,矛盾.
若a-1<-$\frac{1}{2}$,即a<$\frac{1}{2}$,则由不等式可得a<(a-1)2+(a-1)-1,即a2-2a-1>0,求得a>1+$\sqrt{2}$,或a<1-$\sqrt{2}$,
∴a<1-$\sqrt{2}$.
(2)当a-1<x≤a时,不等式化为x2+x+1-a>2(a-x),即${(x+\frac{3}{2})}^{2}$-$\frac{5}{4}$>3a,
若a-1<-$\frac{3}{2}$≤a,即-$\frac{3}{2}$≤a<-$\frac{1}{2}$,此时3a<-$\frac{5}{4}$,a<-$\frac{5}{12}$,结合条件,得-$\frac{3}{2}$≤a<-$\frac{1}{2}$.
若a-1≥-$\frac{3}{2}$,即a≥-$\frac{1}{2}$,3a≤(a-1)2+3(a-1)+1,即a2-2a-1>0,解得a≥1+$\sqrt{2}$ 或a≤1-$\sqrt{2}$.
结合条件及(1),得-$\frac{1}{2}$≤a<1-$\sqrt{2}$.
若a<-$\frac{3}{2}$,3a<a2+3a+1恒成立.
综合得a<1-$\sqrt{2}$.
(3)当x>a时,不等式化为x2+x+1>2(x-a),即x2-x+1>-a,解得a>-$\frac{3}{4}$.
结合(2)可得-$\frac{3}{4}$<a<1-$\sqrt{2}$.
所以,使不等式使不等式f(x)>2|x-a|恒成立的a的取值范围是-$\frac{3}{4}$<a<1-$\sqrt{2}$.
故本题所要求的a的取值范围是a≥1-$\sqrt{2}$,或a≤-$\frac{3}{4}$.
点评 本题考查了含有绝对值的函数与不等式的应用问题,解题时应利用转化思想,再讨论函数的性质与解不等式,是较难的题目.


 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
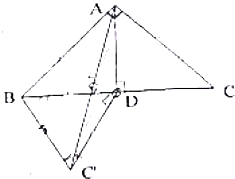 如图,在△ABC中,∠BAC=90°,AB=AC=2,AD⊥BC于D.将△ADC沿AD翻折至△ADC′,下列说法中正确的是①③④(写出所有正确命题的序号)
如图,在△ABC中,∠BAC=90°,AB=AC=2,AD⊥BC于D.将△ADC沿AD翻折至△ADC′,下列说法中正确的是①③④(写出所有正确命题的序号)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
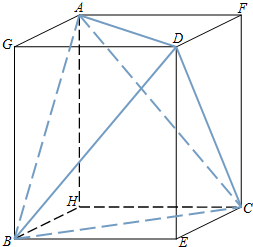 如图,长宽高分别为a、b、c的长方体的六条面对角线组成等腰四面体ABCD.
如图,长宽高分别为a、b、c的长方体的六条面对角线组成等腰四面体ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com