
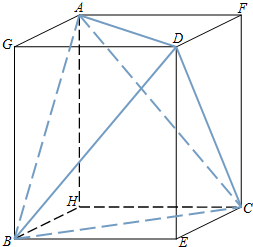
 如图,长宽高分别为a、b、c的长方体的六条面对角线组成等腰四面体ABCD.
如图,长宽高分别为a、b、c的长方体的六条面对角线组成等腰四面体ABCD.分析 (1)利用余弦定理,即可证明;
(2)利用割补法求体积,求出外接球半径,即可求出外接球的表面积.
解答 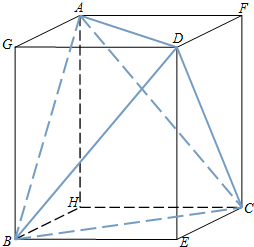 (1)证明:易知四个面是全等的三角形.
(1)证明:易知四个面是全等的三角形.
三边长分别为$x=\sqrt{{b^2}+{c^2}}$,$y=\sqrt{{c^2}+{a^2}}$,$z=\sqrt{{a^2}+{b^2}}$,
不妨设a≤b≤c,则最大边x所对角θ 的余弦值$cosθ=\frac{{{y^2}+{z^2}-{x^2}}}{2yz}=\frac{a^2}{{\sqrt{{a^2}+{b^2}}\sqrt{{c^2}+{a^2}}}}>0$
∴θ 为锐角,
∴三角形为锐角三角形.(4分)
(2)解:体积$V=abc-4×\frac{1}{3}×\frac{1}{2}abc=\frac{1}{3}abc$(7分)
外接球半径$R=\frac{1}{2}BF=\frac{1}{2}\sqrt{{a^2}+{b^2}+{c^2}}$
外接球的表面积S=4πR2=π(a2+b2+c2).(10分)
点评 本题考查余弦定理的运用,考查学生的计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | 0 | D. | $-\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(1)<f(-1)<c | B. | f(-1)<c<f(1) | C. | f(1)<c<f(3) | D. | c<f(3)<f(1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 底面是矩形的平行六面体是长方体 | |
| B. | 底面是正方形的直平行六面体是正四棱柱 | |
| C. | 底面是正方形的直四棱柱是正方体 | |
| D. | 所有棱长都相等的直平行六面体是正方体 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 是奇函数但不是偶函数 | B. | 是偶函数但不是奇函数 | ||
| C. | 既是奇函数又是偶函数 | D. | 既不是奇函数又不是偶函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com