
分析 (1)根据离心率和通径的值列方程组求解得基本量a,b.
(2)巧设方程,避免分类讨论.联立直线和椭圆方程,根据韦达定理得出三角形面积的表达式,并根据基本不等式求得面积最大值,及取面积最大值时的直线斜率,再写出直线方程.
解答 解:(1)由题可知$\left\{{\begin{array}{l}{\frac{c}{a}=\frac{{2\sqrt{5}}}{5}}\\{\frac{{2{b^2}}}{a}=\frac{{2\sqrt{5}}}{5}}\end{array}}\right.$.解得$a=\sqrt{5},c=2$
所以b=1,所以椭圆方程为$\frac{{x}^{2}}{5}+{y}^{2}=1$…(4分)
(2)由题意,可设直线l的方程为x=my+2,
则点M到直线l的距离$d=\frac{8}{{\sqrt{1+{m^2}}}}$.
由$\left\{\begin{array}{l}{x=my+2}\\{\frac{{x}^{2}}{5}+{y}^{2}=1}\end{array}\right.$ 得(m2+5)y2+4my-1=0.
设l与E的两个交点坐标分别为(x1,y1),(x2,y2),
则y1+y2=$-\frac{4m}{{m}^{2}+5}$,y1y2=$-\frac{1}{{m}^{2}+5}$.
于是AB=$\sqrt{(1+{m}^{2})}|{y}_{1}-{y}_{2}|$
=$\sqrt{(1+{m}^{2})[({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}]}$
=$\sqrt{(1+{m}^{2})[\frac{16{m}^{2}}{({m}^{2}+5)^{2}}+\frac{4}{{m}^{2}+5}]}$
=$\frac{2\sqrt{5}({m}^{2}+1)}{{m}^{2}+5}$.
从而S=$\frac{8\sqrt{5}•\sqrt{{m}^{2}+1}}{{m}^{2}+5}$
令$t=\sqrt{{m}^{2}+1}$(t≥1)则m2=t2-1
S=$\frac{8\sqrt{5}t}{{t}^{2}+4}$=$\frac{8\sqrt{5}}{t+\frac{4}{t}}$$≤\frac{8\sqrt{5}}{4}$=2$\sqrt{5}$.
当且仅当$t=\frac{4}{t}$即 $\sqrt{m2+1}$=$\frac{4}{\sqrt{m2+1}}$,即m=±$\sqrt{3}$时,等号成立.
故当m=±$\sqrt{3}$时,S最大,
此时,直线l的方程为x=$\sqrt{3}$y+2或x=-$\sqrt{3}$y+2,即x-$\sqrt{3}$y-2=0或x+$\sqrt{3}$y-2=0.…(12分)
点评 考查了椭圆基本性质,直线与椭圆位置关系,圆锥曲线中三角形面积的求解方法,基本不等式求最值.考查了方程思想,换元法,整体代换.思路不难找,有一定运算量,属于圆锥曲线的中档题.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:解答题
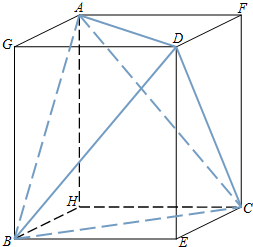 如图,长宽高分别为a、b、c的长方体的六条面对角线组成等腰四面体ABCD.
如图,长宽高分别为a、b、c的长方体的六条面对角线组成等腰四面体ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | e2015•f(2016)>e2016•f(2015) | |
| B. | e2016•f(2016)=e2016•f(2015) | |
| C. | e2015•f(2016)<e2016•f(2015) | |
| D. | e2015•f(2016)与e2016•f(2015)大小不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 优秀 | 非优秀 | 总计 | |
| 甲班 | 10 | ||
| 乙班 | 30 | ||
| 合计 | 105 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,线段AB在平面α内,线段AC⊥α,线段BD⊥AB,且AB=1,AC=BD=4,BD与α所成角的正弦值为$\frac{1}{4}$,则CD=( )
如图,线段AB在平面α内,线段AC⊥α,线段BD⊥AB,且AB=1,AC=BD=4,BD与α所成角的正弦值为$\frac{1}{4}$,则CD=( )| A. | 5 | B. | $\frac{11}{2}$ | C. | 6 | D. | 7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com