
分析 (1)由f(x)的图象关于点(1,0)成中心对称,则f(1+x)=-f(1-x)⇒6(1-a)x2+12(a-1)x+(2-a)3-a3=0对x∈R恒成立,即可求a.
(2)利用导数求函数单调区间,再求最值即可.
解答 解:(1)法1:化简f(x)得f(x)=(x-a)3 (1分)
由f(x)的图象关于点(1,0)成中心对称,则f(1+x)=-f(1-x)…(2分)
即f(x)=-f(2-x)…,代入f(x)得(x-a)3+(2-x-a)3=0,整理得:
6(1-a)x2+12(a-1)x+(2-a)3-a3=0对x∈R恒成立,则
$\left\{\begin{array}{l}{6-6a=0}\\{12a-12=0}\\{(2-a)3-a3=0}\end{array}\right.∴a=1,\\;f(x)=(x-1)^{3}$ (6分)
法2:f(x)=x3是奇函数,f(x)=(x-a)3
是将f(x)的图象向左(a<0)或向右(a>0)平移|a|个单位,
由题意平移后的图象关于点(1,0)成中心对称,故a=1.
(2)g(x)=f(x)-2x2=(x-1)3-2x2,
∵g′(x)=3x2-10x+3=0,∴${x}_{1}=\frac{1}{3},{x}_{2}=3$,又x∈[-1,1],
则x∈[-1,$\frac{1}{3}$]时g(x)递增,x∈[$\frac{1}{3},1$]时g(x)递减,故g(x)max=g($\frac{1}{3}$)=-$\frac{14}{27}$,
g(-1)=-10,g(1)=-2,∴g(x)min=-10.(10分)
综上,g(x)max=$\frac{14}{27}$,g(x)min=-10.(12分)
点评 本题考查了函数的对称性及最值,关键是把对称的定性描述转化为定量运算,属于基础题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | f(1)<f(-1)<c | B. | f(-1)<c<f(1) | C. | f(1)<c<f(3) | D. | c<f(3)<f(1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 是奇函数但不是偶函数 | B. | 是偶函数但不是奇函数 | ||
| C. | 既是奇函数又是偶函数 | D. | 既不是奇函数又不是偶函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,0)∪(2,+∞) | B. | (-2,0)∪(0,2) | C. | (-∞,-2)∪(2,+∞) | D. | (-∞,-2)∪(0,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 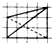 | B. | 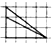 | C. | 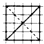 | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,直三棱柱ABC-A1B1C1内接于高为$\sqrt{2}$的圆柱中,已知∠ACB=90°,AA1=$\sqrt{2}$,BC=AC=1,O为AB的中点.求:
如图,直三棱柱ABC-A1B1C1内接于高为$\sqrt{2}$的圆柱中,已知∠ACB=90°,AA1=$\sqrt{2}$,BC=AC=1,O为AB的中点.求:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com