
���� ��1����������W=�����x��ÿǧ������������ΪR��x��-�ɱ�������R��x��=$\left\{\begin{array}{l}{9.4-\frac{1}{30}{x}^{2}��0��x��10��}\\{\frac{110}{x}-\frac{432}{{x}^{2}}��x��10��}\end{array}\right.$������̶��ɱ�Ϊ10��Ԫ��ÿ����1ǧ������Ͷ��3��Ԫ��������������W����Ԫ�����������x��ǧ�����ĺ�������ʽ��
��2���ɣ�1���Ľ���ʽ��������������ϵ����ֵ������������ֵ��Ȼ����ݷֶκ��������ֵ�Ǹ��������ֵ������ߣ����ɵõ������
��� �⣺��1����0��x��10ʱ��
$W=xR��x��-��10+3x��=x��9.4-\frac{1}{30}{x^2}��-10-3x=6.4x-\frac{x^3}{30}-10$��
��x��10ʱ��$W=xR��x��-��10+3x��=x��\frac{110}{x}-\frac{432}{x^2}��-10-3x=100-3��x+\frac{144}{x}��$��
����W=$\left\{\begin{array}{l}{6.4x-\frac{{x}^{3}}{30}-10��x�ʣ�0��10]}\\{100-3��x+\frac{144}{x}����x�ʣ�10��+�ޣ�}\end{array}\right.$��
��2���ٵ�0��x��10ʱ����W'=6.4-$\frac{{x}^{2}}{10}$=0����x=8��
�ҵ�x�ʣ�0��8��ʱ��W'��0����x�ʣ�8��10��ʱ��W'��0��
�൱x=8ʱ��Wȡ���ֵ����Wmax=6.4��8-$\frac{{8}^{3}}{30}$-10��24��
�ڵ�x��10ʱ��W=100-3��x+$\frac{144}{x}$����100-3��2$\sqrt{x•\frac{144}{x}}$=100-72=28��
���ҽ���x=$\frac{144}{x}$����x=12ʱ��W=28��
�ʵ�x=12ʱ��Wȡ���ֵ28��
�ۺϢ٢�֪��x=12ʱ��Wȡ���ֵ28��Ԫ��
�ʵ������Ϊ12ǧ��ʱ���ù�˾����һƷ�Ʒ�װ���������������������
���� ���⿼���֪ʶ���Ƿֶκ�������������ֵ���ֶκ����ֶδ����������о��ֶκ���ͼ�����������ĵ�������������ǣ��ֶκ����Ķ�����ֵ���Ǹ�����x��yȡֵ��Χ�IJ������ֶκ�������ż�ԡ�������Ҫ�ڸ����Ϸֱ���֤���ֶκ��������ֵ���Ǹ��������ֵ�е�����ߣ�


 ����ѧ���ʱѧ����ϵ�д�
����ѧ���ʱѧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ���溯��������ż���� | B�� | ��ż�����������溯�� | ||
| C�� | �����溯������ż���� | D�� | �Ȳ����溯���ֲ���ż���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ƽ��ֱ������ϵxOy�У���֪��ԲC��$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;��a��b��0��$���ҽ���Ϊ$��\sqrt{2}��0��$���Ҿ�����$��\frac{{\sqrt{2}}}{2}��-\frac{{\sqrt{7}}}{2}��$������Բ����A��ֱ��l��x�ᣬ��MΪֱ��l�ϵĶ��㣨��M���A���غϣ�����BΪ��Բ�Ҷ��㣬ֱ��BM����ԲC�ڵ�P��
��ƽ��ֱ������ϵxOy�У���֪��ԲC��$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;��a��b��0��$���ҽ���Ϊ$��\sqrt{2}��0��$���Ҿ�����$��\frac{{\sqrt{2}}}{2}��-\frac{{\sqrt{7}}}{2}��$������Բ����A��ֱ��l��x�ᣬ��MΪֱ��l�ϵĶ��㣨��M���A���غϣ�����BΪ��Բ�Ҷ��㣬ֱ��BM����ԲC�ڵ�P���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-2��0���ȣ�2��+�ޣ� | B�� | ��-2��0���ȣ�0��2�� | C�� | ��-�ޣ�-2���ȣ�2��+�ޣ� | D�� | ��-�ޣ�-2���ȣ�0��2�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 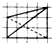 | B�� | 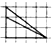 | C�� | 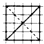 | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com