
分析 (1)将函数表示为分段函数形式,然后进行作图即可,
(2)利用不等式恒成立,转化为最值恒成立即可.
解答 解:(1)y=f(x)=$\left\{\begin{array}{l}{2x-3,}&{x≥2}\\{5-2x,}&{x<2}\end{array}\right.$,则对应的函数图象为:
(2)∵f(x)=|2x-4|+1≥1,
∴若对任意x∈R,f(x)≥a2-3a恒成立,
则等价为a2-3a≤1,即a2-3a-1≤0,
得$\frac{3-\sqrt{13}}{2}$<a<$\frac{3+\sqrt{13}}{2}$,
即实数a的取值范围是$\frac{3-\sqrt{13}}{2}$<a<$\frac{3+\sqrt{13}}{2}$.
点评 本题主要考查函数图象的应用,以及不等式恒成立问题,将函数表示为分段函数形式以及利用最值恒成立是解决本题的关键.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
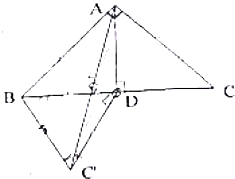 如图,在△ABC中,∠BAC=90°,AB=AC=2,AD⊥BC于D.将△ADC沿AD翻折至△ADC′,下列说法中正确的是①③④(写出所有正确命题的序号)
如图,在△ABC中,∠BAC=90°,AB=AC=2,AD⊥BC于D.将△ADC沿AD翻折至△ADC′,下列说法中正确的是①③④(写出所有正确命题的序号)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
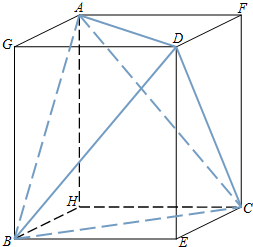 如图,长宽高分别为a、b、c的长方体的六条面对角线组成等腰四面体ABCD.
如图,长宽高分别为a、b、c的长方体的六条面对角线组成等腰四面体ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 28 | B. | 21 | C. | 36 | D. | 32 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 优秀 | 非优秀 | 总计 | |
| 甲班 | 10 | ||
| 乙班 | 30 | ||
| 合计 | 105 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com