

| A. | 28 | B. | 21 | C. | 36 | D. | 32 |
分析 观察不难发现,第n个三角形所表示的数为从1开始到n的自然数的和,然后相加即可得解.
解答 解:第1个三角形表示的数是1,
第2个三角形表示的数是1+2=3,
第3个三角形表示的数是1+2+3=6,
第4个三角形表示的数是1+2+3+4=10,
…,
第n个三角形表示的数是1+2+3+…+n=$\frac{1}{2}$n(n+1)
∴第七个三角形表示的数是$\frac{1}{2}$×7×8=28.
故选:A.
点评 本题考查数列的递推关系,数列的求和及归纳推理,解题的关键是由题设得出相邻两个三角形数的递推关系,由此列举出三角形数,本题综合性强,有一定的探究性,是高考的重点题型,解答时要注意总结其中的规律.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 底面是矩形的平行六面体是长方体 | |
| B. | 底面是正方形的直平行六面体是正四棱柱 | |
| C. | 底面是正方形的直四棱柱是正方体 | |
| D. | 所有棱长都相等的直平行六面体是正方体 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 是奇函数但不是偶函数 | B. | 是偶函数但不是奇函数 | ||
| C. | 既是奇函数又是偶函数 | D. | 既不是奇函数又不是偶函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在平面直角坐标系xOy中,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;(a>b>0)$的右焦点为$(\sqrt{2},0)$,且经过点$(\frac{{\sqrt{2}}}{2},-\frac{{\sqrt{7}}}{2})$,过椭圆的左顶点A作直线l⊥x轴,点M为直线l上的动点(点M与点A不重合),点B为椭圆右顶点,直线BM交椭圆C于点P.
在平面直角坐标系xOy中,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;(a>b>0)$的右焦点为$(\sqrt{2},0)$,且经过点$(\frac{{\sqrt{2}}}{2},-\frac{{\sqrt{7}}}{2})$,过椭圆的左顶点A作直线l⊥x轴,点M为直线l上的动点(点M与点A不重合),点B为椭圆右顶点,直线BM交椭圆C于点P.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 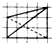 | B. | 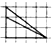 | C. | 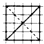 | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com