
分析 (I)依次把n=1,2,3代入Sn+an=2计算即可;
(II)先验证n=1,再假设n=k猜想成立,推导n=k+1成立即可.
解答 解:(I)由题意Sn+an=2,
∴a1=1,a2=$\frac{1}{2}$,a3=$\frac{1}{4}$.
(II)猜想:an=$\frac{1}{{2}^{n-1}}$.
下面用数学归纳法证明:
①当n=1时,a1=1,$\frac{1}{{2}^{1-1}}$=$\frac{1}{{2}^{0}}$=1,猜想成立.
②假设当n=k时,等式成立,即ak=$\frac{1}{{2}^{k-1}}$,
则当n=k+1时,由Sk+1+ak+1=2,Sk+ak=2,
得(Sk+1-Sk)+ak+1-ak=0,
即2ak+1=ak,
∴ak+1=$\frac{1}{2}$ak=$\frac{1}{{2}^{k}}$,
∴当n=k+1时,猜想也成立,
∴对于任意n∈N+,an=$\frac{1}{{2}^{n-1}}$.
点评 本题考查了数学归纳法证明,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | α∥β | B. | α⊥β | ||
| C. | α,β相交但不垂直 | D. | α,β所成的锐二面角为60° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
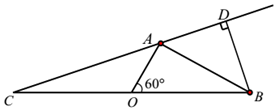 随着节假日外出旅游人数增多,倡导文明旅游的同时,生活垃圾处理也面临新的挑战,某海滨城市沿海有A,B,C三个旅游景点,在岸边BC两地的中点处设有一个垃圾回收站点O(如图),A,B两地相距10km,从回收站O观望A地和B地所成的视角为60°,且${\overrightarrow{OA}^2}+{\overrightarrow{OB}^2}≥4\overrightarrow{OA}•\overrightarrow{OB}$,设AC=xkm;
随着节假日外出旅游人数增多,倡导文明旅游的同时,生活垃圾处理也面临新的挑战,某海滨城市沿海有A,B,C三个旅游景点,在岸边BC两地的中点处设有一个垃圾回收站点O(如图),A,B两地相距10km,从回收站O观望A地和B地所成的视角为60°,且${\overrightarrow{OA}^2}+{\overrightarrow{OB}^2}≥4\overrightarrow{OA}•\overrightarrow{OB}$,设AC=xkm;查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,矩形ADFE,矩形CDFG,正方形ABCD两两垂直,且AB=2,若线段DE上存在点P使得GP⊥BP,则边CG长度的最小值为 ( )
如图,矩形ADFE,矩形CDFG,正方形ABCD两两垂直,且AB=2,若线段DE上存在点P使得GP⊥BP,则边CG长度的最小值为 ( )| A. | 4 | B. | $4\sqrt{3}$ | C. | 2 | D. | $2\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a>b,则ac2>bc2 | |
| B. | 实数a,b,c满足b2=ac,则a,b,c成等比数列 | |
| C. | 若$θ∈({0,\frac{π}{2}})$,则$y=sinθ+\frac{2}{sinθ}$的最小值为$2\sqrt{2}$ | |
| D. | 若数列{n2+λn}为递增数列,则λ>-3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com