
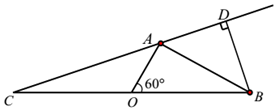
 随着节假日外出旅游人数增多,倡导文明旅游的同时,生活垃圾处理也面临新的挑战,某海滨城市沿海有A,B,C三个旅游景点,在岸边BC两地的中点处设有一个垃圾回收站点O(如图),A,B两地相距10km,从回收站O观望A地和B地所成的视角为60°,且${\overrightarrow{OA}^2}+{\overrightarrow{OB}^2}≥4\overrightarrow{OA}•\overrightarrow{OB}$,设AC=xkm;
随着节假日外出旅游人数增多,倡导文明旅游的同时,生活垃圾处理也面临新的挑战,某海滨城市沿海有A,B,C三个旅游景点,在岸边BC两地的中点处设有一个垃圾回收站点O(如图),A,B两地相距10km,从回收站O观望A地和B地所成的视角为60°,且${\overrightarrow{OA}^2}+{\overrightarrow{OB}^2}≥4\overrightarrow{OA}•\overrightarrow{OB}$,设AC=xkm;分析 (1)根据OC=BO,分别在△OAC与△OAB中利用余弦定理,可得x2=OA2+OB2+OA•OB且100=OA2+OB2-OA•OB.两式联解即可得出用x表示OA2+OB2、OA•OB的式子,再根据基本不等式与实际问题有意义建立关于x的不等式组,解之即可得到x的取值范围;
(2)根据AO是△AOB的中线,利用三角形的面积公式算出S△ABC=2S△AOB=$\frac{1}{2}$•AC•BD,解出BD=$\frac{\sqrt{3}({x}^{2}-100)}{2x}$,设BD=f(x),由于f(x)在区间(10,10$\sqrt{3}$]上是增函数,可得当x=10$\sqrt{3}$时,f(x)有最大值,由此可得当AC=10$\sqrt{3}$时BD的最大值为10.
解答  解:(1)在△OAC中,∠AOC=120°,AC=x,
解:(1)在△OAC中,∠AOC=120°,AC=x,
由余弦定理得,OA2+OC2-2OA•OC•cos120°=x2,
又OC=BO,
所以OA2+OB2-2OA•OB•cos120°=x2①
在△OAB中,AB=10,∠AOB=60°
由余弦定理得,OA2+OB2-2OA•OB•cos60°=100②
①+②得$O{A^2}+O{B^2}=\frac{{{x^2}+100}}{2}$,可得:${\overrightarrow{OA}^2}+{\overrightarrow{OB}^2}$=$\frac{{x}^{2}+100}{2}$,
①-②得4OA•OB•cos60°=x2-100,
又因为:${\overrightarrow{OA}^2}+{\overrightarrow{OB}^2}≥4\overrightarrow{OA}•\overrightarrow{OB}$,
所以$\frac{{x}^{2}+100}{2}$≥x2-100,即x2≤300,
又$\overrightarrow{OA}•\overrightarrow{OB}$=$\frac{{x}^{2}-100}{4}$>0,即x2>100,
所以$10<x≤10\sqrt{3}$.
(2))∵O是BC的${S_{△ABC}}=\frac{1}{2}•AC•BD$中点,可得S△OAB=S△OAC,
故${S_{△ABC}}=2{S_{△OAB}}=2•\frac{1}{2}•OA•OBsin{60^0}=\frac{{\sqrt{3}({x^2}-100)}}{4}$,
又,
∴$\frac{1}{2}$•x•BD=$\frac{\sqrt{3}}{4}$(x2-100),得BD=$\frac{\sqrt{3}({x}^{2}-100)}{2x}$.
设BD=f(x),
所以$f(x)=\frac{{\sqrt{3}({x^2}-100)}}{2x}$,$x∈(10,10\sqrt{3}]$,
又$f(x)=\frac{{\sqrt{3}}}{2}(x-\frac{100}{x})$,y=x,$y=-\frac{100}{x}$在$(10,10\sqrt{3}]$上都是增函数;
所以,f(x)在$(10,10\sqrt{3}]$上是增函数,
所以f(x)的最大值为$f(10\sqrt{3})=10$,即BD的最大值为10.
(利用单调性定义证明f(x)在$(10,10\sqrt{3}]$上是增函数,同样给满分;如果直接说出f(x)在$(10,10\sqrt{3}]$上是增函数,但未给出证明或讨论,扣1分)
点评 本题给出实际应用问题,求BD的最大值,着重考查了余弦定理、三角形的面积公式、二次函数的单调性等知识,考查了解三角形知识在实际问题中的应用,属于中档题.


科目:高中数学 来源: 题型:解答题
 如图所示的三棱锥P-ABC中,∠BAC=90°,PA⊥平面ABC,AB=AC=2,PA=4,E,F,G分别为棱PB,BC,AC的中点,点H在棱AP上,AH=1.
如图所示的三棱锥P-ABC中,∠BAC=90°,PA⊥平面ABC,AB=AC=2,PA=4,E,F,G分别为棱PB,BC,AC的中点,点H在棱AP上,AH=1.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{6}$ | B. | 6 | C. | $\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{2}$ | B. | $-\frac{5}{2}$ | C. | $±\frac{15}{4}$ | D. | $±\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com